
分析 由题意可知直线经过圆的圆心,推出a,b的关系,利用(a,b)与圆心的距离,半径,求出切线长的表达式,然后求出最小值.
解答 解:若圆C:(x+1)2+(y-2)2=8的圆心坐标为(-1,2)半径为2$\sqrt{2}$.
圆C:(x+1)2+(y-2)2=8关于直线2ax+by+6=0对称,所以(-1,2)在直线上,可得-2a+2b+6=0,
即a=b+3.
所以点(a,b)向圆C所作切线长:$\sqrt{(a+1)^{2}+(b-2)^{2}-8}$=$\sqrt{2(a-2)^{2}+10}$≥$\sqrt{10}$
当且仅当a=2时弦长最小,为$\sqrt{10}$.
故答案为$\sqrt{10}$.
点评 本题考查直线与圆的位置关系,对称问题,圆的切线方程的应用,考查计算能力.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
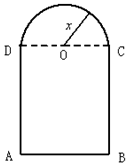 如图,用长为12m的铁丝弯成下部为矩形,上部为半圆形的框架窗户,若半圆半径
如图,用长为12m的铁丝弯成下部为矩形,上部为半圆形的框架窗户,若半圆半径查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 商品名称 | A | B | C | D | E |
| 销售额x(千万元) | 3 | 5 | 6 | 7 | 9 |
| 利润额y(百万元) | 2 | 3 | 3 | 4 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 1+i | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
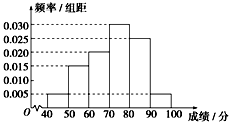 某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩 (均为整数)的频率分布直方图如图所示.估计这次测试中数学成绩的平均分为72,众数为75.
某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩 (均为整数)的频率分布直方图如图所示.估计这次测试中数学成绩的平均分为72,众数为75.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com