练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    若实数x，y满足条件
    x-1≥0
    x-2y+3≥0
    x-y≤0
    ，则x+2y的最小值等于（　　）
    A、3B、4C、5D、9
    考点：简单线性规划
    专题：数形结合,不等式的解法及应用
    分析：先画出可行域，然后做出直线l：x+2y=0，再通过平移的方法求出z=x+2y的最小值．
    解答： 解：作出满足条件
    x-1≥0
    x-2y+3≥0
    x-y≤0
    的可行域如下图中的阴影部分：
    作出直线l：x+2y=0，对于可行域内所有的点来说，将此直线平移过A点时，z=x+2y的值最小，
    由
    x=1
    x-y=0
    得A（1，1），
    ∴zmin=3．
    故选：A
    点评：这是一道线性规划问题，重点考查可行域的画法以及目标函数最值的求法，要在充分理解目标函数z的几何意义的基础上解决此类问题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    若曲线y=x3在点（1，1）处的切线和曲线y=ax2+10x-9也相切，则实数a的值为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在集合{1，2，3，4，5}中任取一个偶数a和一个奇数b构成以原点为起点的向量
    a
    =（a，b），从所有得到的以原点为起点的向量中任取两个向量为邻边作平行四边形，记所有作成的平行四边形的个数为t，在区间（1，
    t
    3
    ）和（2，4）内分别各取一个数，记为m和n，则方程
    x2
    m2
    +
    y2
    n2
    =1表示焦点在x轴上的椭圆的概率P为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，ABCD-A1B1C1D1是正方体，在底面A1B1C1D1上任取一点M，则∠MAA1≤
    π
    6
    的概率P=（　　）
    A、
    π
    15
    B、
    π
    12
    C、
    π
    9
    D、
    π
    6

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知Z为整数集，集合U={x∈Z|x2-6x≥0}，集合M满足M⊆∁ZU，且M∩{1，2，3}={1，2}，则M的个数是（　　）
    A、1B、2C、3D、4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    定义在R上的可导函数f（x），若x≠1时，（x-1）f′（x）＜0恒成立（其中f′（x）是f（x）的导函数），则下列各项中一定正确的是（　　）
    A、f（0）+f（2）＞2 f（1）
    B、f（0）+f（2）=2f（1）
    C、f（0）+f（2）＜2 f（1）
    D、不能确定

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若sinα+2icosα=2i，则α的取值范围为（　　）
    A、{α|α=kπ，k∈Z}
    B、{α|α=
    kπ
    2
    ，k∈Z}
    C、{α|α=2kπ，k∈Z}
    D、{α|α=2kπ+
    π
    2
    ，k∈Z}

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知集合S={x||x-1|≤2，x∈R}，T={x|
    5
    x+1
    ≥0，x∈Z}，则S∩T=（　　）
    A、{x|0＜x＜3，x∈Z}
    B、{x|0≤x≤3，x∈Z}
    C、{x|-1≤x≤3，x∈Z}
    D、{x|-1＜x＜3，x∈Z}

    查看答案和解析>>

    科目：高中数学 来源： 题型：

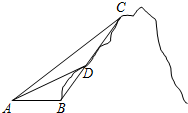    某旅游景点有一座风景秀丽的山峰，游客可以乘长为3km的索道AC上山，也可以沿山路BC上山，山路BC中间有一个距离山脚B为1km的休息点D．已知∠ABC=120°，∠ADC=150°．假设小王和小李徒步攀登的速度为每小时1.2km，请问：两位登山爱好者能否在2个小时内徒步登上山峰（即从B点出发到达C点）

    查看答案和解析>>

    同步练习册答案