
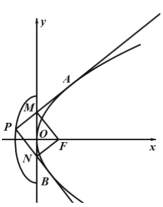
【题目】如图,设抛物线![]() 的焦点为F,点P是半椭圆
的焦点为F,点P是半椭圆![]() 上的一点,过点P作抛物线C的两条切线,切点分别为A、B,且直线PA、PB分别交y轴于点M、N.
上的一点,过点P作抛物线C的两条切线,切点分别为A、B,且直线PA、PB分别交y轴于点M、N.
(1)证明:![]() ;
;
(2)求![]() 的取值范围.
的取值范围.
【答案】(1)证明见解析 (2)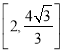
【解析】
(1)设点P的坐标为![]() ,由直线PA与椭圆相切,得
,由直线PA与椭圆相切,得![]() ,要证明
,要证明![]() ,只需证明
,只需证明![]() ,即证
,即证![]() 即可;
即可;
(2)![]() ,
,![]() ,
,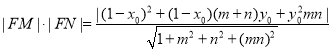 ,由(1)易得
,由(1)易得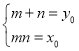 ,代入化简即可.
,代入化简即可.
(1)由题意知,直线PA的斜率存在且不为0,设点P的坐标为![]() ,
,
直线PA方程为![]() .
.
令![]() ,可知点M的坐标为
,可知点M的坐标为![]() .
.
由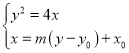 ,消去x得
,消去x得![]() .
.
因为直线与抛物线只有一个交点,
故![]() ,即
,即![]() .
.
因为点F的坐标为![]() ,
,
故![]() ,
,![]() .
.
则![]() .
.
因此![]() ,亦即
,亦即![]() .
.
(2)设直线PB的方程为![]() .
.
由(1)可知,n满足方程![]() .
.
故m,n是关于t的方程![]() 的两个不同的实根.
的两个不同的实根.
所以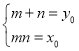 .
.
由(1)可知:![]() ,同理可得
,同理可得![]() .
.
故![]() ,
,![]() .
.
则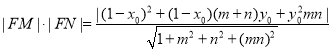 ,
,
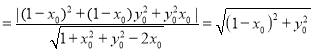
因为![]() ,
,
所以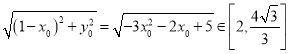 .
.
因此,![]() 的取值范围是
的取值范围是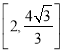 .
.
【点晴】
本题考查直线与椭圆的位置关系,计算量较大,考查学生的运算求解能力、转化与化归的思想,是一道中档题.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源: 题型:
【题目】已知极点与平面直角坐标系的原点重合,极轴与![]() 轴的正半轴重合,直线
轴的正半轴重合,直线![]() 的参数方程为
的参数方程为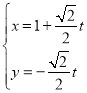 (
(![]() 是参数),曲线
是参数),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 为曲线
为曲线![]() 上一点,求使
上一点,求使![]() 面积取得最大值时的
面积取得最大值时的![]() 点坐标.
点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某产品的广告支出![]() (单位:万元)与销售收入
(单位:万元)与销售收入![]() (单位:万元)之间有下表所对应的数据:
(单位:万元)之间有下表所对应的数据:
广告支出 | 1 | 2 | 3 | 4 |
销售收入 | 12 | 28 | 42 | 56 |
(1)画出表中数据的散点图;
(2)求出![]() 对
对![]() 的线性回归方程;
的线性回归方程;
(3)若广告费为9万元,则销售收入约为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现安排6名同学前往4所学校进行演讲,要求甲、乙两同学不能前往同一个学校,每个学校都有人前往,每人只前往一个学校,则满足上述要求的不同安排方案数为________.(用数字作答)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() ,离心率为
,离心率为![]() .设过点
.设过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于不同两点
相交于不同两点![]() ,
, ![]() 周长为
周长为![]() .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)已知点![]() ,证明:当直线
,证明:当直线![]() 变化时,总有TA与
变化时,总有TA与![]() 的斜率之和为定值.
的斜率之和为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】先后2次抛掷一枚骰子,将得到的点数分别记为![]() ,
,![]() .
.
(1)求直线![]() 与圆
与圆![]() 相切的概率;
相切的概率;
(2)将![]() ,
,![]() ,5的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
,5的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个口袋中装有![]() 个白球和
个白球和![]() 个黑球,下列事件中,是独立事件的是( )
个黑球,下列事件中,是独立事件的是( )
A.第一次摸出的是白球与第一次摸出的是黑球
B.摸出后放回,第一次摸出的是白球,第二次摸出的是黑球
C.摸出后不放回,第一次摸出的是白球,第二次摸出的是黑球
D.一次摸两个球,共摸两次,第一次摸出颜色相同的球与第一次摸出颜色不同的球
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com