练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】一个口袋中装有个白球和个黑球，下列事件中，是独立事件的是（ ）

    A.第一次摸出的是白球与第一次摸出的是黑球

    B.摸出后放回，第一次摸出的是白球，第二次摸出的是黑球

    C.摸出后不放回，第一次摸出的是白球，第二次摸出的是黑球

    D.一次摸两个球，共摸两次，第一次摸出颜色相同的球与第一次摸出颜色不同的球

    【答案】B

    【解析】

    根据独立事件的定义逐一判断即可得解.

    解：对于选项A，第一次摸出的是白球与第一次摸出的是黑球，是随机事件；

    对于选项B，摸出后放回，第一次摸出的是白球，第二次摸出的是黑球，两者不受影响，是独立事件；

    对于选项C，摸出后放回，第一次摸出的是白球，第二次摸出的是黑球，第二次受第一次的影响，不是独立事件；

    对于选项D，一次摸两个球，共摸两次，第一次摸出颜色相同的球与第一次摸出颜色不同的球，有影响，不是独立事件，

    故选：B.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

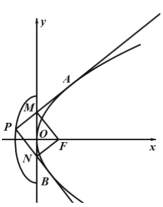
    【题目】如图，设抛物线的焦点为F，点P是半椭圆上的一点，过点P作抛物线C的两条切线，切点分别为A、B，且直线PA、PB分别交y轴于点M、N．

    （1）证明：；

    （2）求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设有关于x的一元二次方程.

    （1）若a是从0、1、2、3四个数中任取的一个数，是从0、1、2三个数中任取的一个数，求上述方程没有实根的概率.

    （2）若a是从区间内任取的一个数，，求上述方程没有实根的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】第十四届全国冬季运动会召开期间，某校举行了“冰上运动知识竞赛”，为了解本次竞赛成绩情况，从中随机抽取部分学生的成绩(得分均为整数，满分100分)进行统计，请根据频率分布表中所提供的数据，解答下列问题：

    （1）求、、的值及随机抽取一考生其成绩不低于70分的概率；

    （2）若从成绩较好的3、4、5组中按分层抽样的方法抽取5人参加“普及冰雪知识”志愿活动，并指定2名负责人，求从第4组抽取的学生中至少有一名是负责人的概率.

    组号

    分组

    频数

    频率

    第1组

    15

    0.15

    第2组

    35

    0.35

    第3组

    b

    0.20

    第4组

    20

    第5组

    10

    0.1

    合计

    1.00

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知,命题:对,不等式恒成立;命题,使得成立.

    (1)若为真命题,求的取值范围;

    (2)当时,若假,为真,求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）讨论的单调性；

    （2）若恒成立，求实数的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆，点为坐标原点，一条直线与圆相切并与椭圆交于不同的两点.

    （1）设，求的表达式；

    （2）若，求直线的方程；

    （3）若，求面积的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司年会举行抽奖活动，每位员工均有一次抽奖机会.活动规则如下：一只盒子里装有大小相同的6个小球，其中3个白球，2个红球，1个黑球，抽奖时从中一次摸出3个小球，若所得的小球同色，则获得一等奖，奖金为300元；若所得的小球颜色互不相同，则获得二等奖，奖金为200元；若所得的小球恰有2个同色，则获得三等奖，奖金为100元.

    （1）求小张在这次活动中获得的奖金数的概率分布及数学期望；

    （2）若每个人获奖与否互不影响，求该公司某部门3个人中至少有2个人获二等奖的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，四棱锥P﹣ABCD中，PC⊥底面ABCD，PC＝CD＝2，E为AB的中点，底面四边形ABCD满足∠ADC＝∠DCB＝90°，AD＝1，BC＝3．

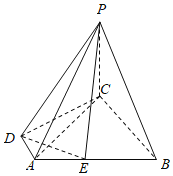
    （Ⅰ）求证：平面PDE⊥平面PAC；

    （Ⅱ）求直线PC与平面PDE所成角的正弦值；

    （Ⅲ）求二面角D﹣PE﹣B的余弦值．

    查看答案和解析>>

    同步练习册答案