
(本题满分14分)
如图,酒杯的形状为倒立的圆锥,杯深8 cm .上口宽6cm , 水以20 cm3/s的流量倒入杯中,当水深为4 cm时,求水升高的瞬时变化率.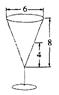
解法一:设时刻t s时,杯中水的体积为Vcm3,水面半径为r cm, 水深为h cm.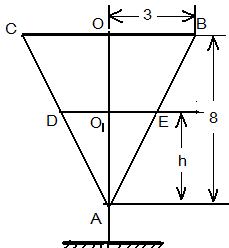
则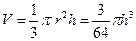 2分
2分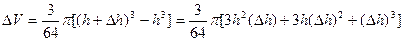 5分
5分 7分
7分
记水升高的瞬时变化率为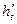 (即当
(即当 无限趋近于0时,
无限趋近于0时, 无限趋近于
无限趋近于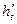 )
)
从而有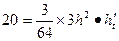 ,当h=4时,解得
,当h=4时,解得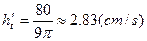 12分
12分
答:当水深为4 cm时,水升高的瞬时变化率为 。 14分
。 14分
解法二:仿解法一,可得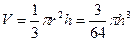 ,即
,即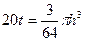 4分
4分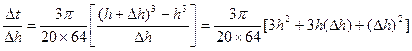 5分
5分
当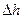 无限趋近于0时,
无限趋近于0时, 无限趋近于
无限趋近于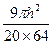 ,即
,即 无限趋近于
无限趋近于 12分
12分
当h=4时,水升高的瞬时变化率是 . 14分
. 14分
解法三:水面高为4 cm时,可求得水面半径为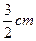 ,设水面高度增加
,设水面高度增加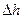 时,水的体积增加
时,水的体积增加 ,从而
,从而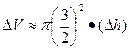 ,(用圆柱近似增加的水体积) , 8分
,(用圆柱近似增加的水体积) , 8分
故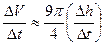 .当
.当 无限趋近于0时得
无限趋近于0时得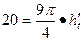 10分
10分
即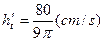 12分
12分
答:当水深为4 cm时,水升高的瞬时变化率为 。 14分
。 14分
解法四:设t 时刻时注入杯中的水的高度为 h ,杯中水面为圆形,其圆半径为r 1分
如图被子的轴截面为等腰三角形ABC,AO1O为底边BC上的高,O1,O 分别为DE,BC中点,
容易求证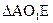 ∽
∽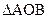 ,那么
,那么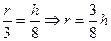 2分
2分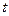 时刻时杯中水的容积为V=
时刻时杯中水的容积为V=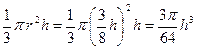 3分
3分
又因为V="20t, " 4分
则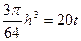 即
即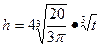 6分
6分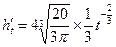 8分
8分
当h="4" 时,设t=t1,
由三角形形似的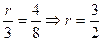 , 9分
, 9分
那么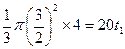
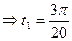 10分
10分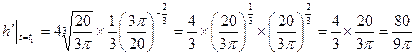 12分
12分
答:当水高为4 cm时,水升高的瞬时变化率为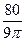 cm/s 14分
cm/s 14分
解析


科目:高中数学 来源: 题型:
(本题满分14分)如图2,为了绿化城市,拟在矩形区域ABCD内建一个矩形草坪,另外△AEF内部有一文物保护区域不能占用,经过测量AB=100m,BC=80m,AE=30m,AF=20m,应该如何设计才能使草坪面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分14分)
如图,已知直三棱柱ABC—A1B1C1,![]() ,E是棱CC1上动点,F是AB中点,
,E是棱CC1上动点,F是AB中点,![]()
(1)求证:![]() ;
;
(2)当E是棱CC1中点时,求证:CF//平面AEB1;
(3)在棱CC1上是否存在点E,使得二面角A—EB1—B的大小是45°,若存在,求CE的长,若不存在,请说明理由。

查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省济宁市高三第二次月考文科数学 题型:解答题
(本题满分14分)如图,在四棱锥E-ABCD中,底面ABCD为正方形, AE⊥平面CDE,已知AE=3,DE=4.

(Ⅰ)若F为DE的中点,求证:BE//平面ACF;
(Ⅱ)求直线BE与平面ABCD所成角的正弦值
查看答案和解析>>
科目:高中数学 来源:2011年福建省高二上学期期末考试数学理卷 题型:解答题
(本题满分14分)如图,正方形 、
、 的边长都是1,平面
的边长都是1,平面
 平面
平面 ,点
,点 在
在 上移动,点
上移动,点 在
在 上移动,若
上移动,若 (
( )
)

(I)求 的长;
的长;
(II) 为何值时,
为何值时, 的长最小;
的长最小;
(III)当 的长最小时,求面
的长最小时,求面 与面
与面 所成锐二面角余弦值的大小.
所成锐二面角余弦值的大小.
查看答案和解析>>
科目:高中数学 来源:杭州市2010年第二次高考科目教学质量检测 题型:解答题
(本题满分14分)如图,矩形BCC1B1所在平面垂直于三角形ABC所在平面,BB1=CC1=AC=2, ,又E、F分别是C1A和C1B的中点。
,又E、F分别是C1A和C1B的中点。
 (1)求证:EF//平面ABC;
(1)求证:EF//平面ABC;
(2)求证:平面 平面C1CBB1;
平面C1CBB1;
(3)求异面直线AB与EB1所成的角。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com