
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:填空题
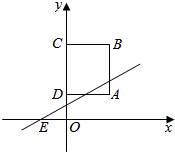 如图:点A的坐标为(2,1),正方形ABCD的点C、点D都在y轴上.从背面完全一样,正面分别写有数字-2,-1,0,1,2的五张牌中任取一张,将其正面的数字作为k值,则能使一次函数y=kx+b的图象过经点E(-1,0),且与正方形ABCD恰有两个公共点的概率是$\frac{2}{5}$.
如图:点A的坐标为(2,1),正方形ABCD的点C、点D都在y轴上.从背面完全一样,正面分别写有数字-2,-1,0,1,2的五张牌中任取一张,将其正面的数字作为k值,则能使一次函数y=kx+b的图象过经点E(-1,0),且与正方形ABCD恰有两个公共点的概率是$\frac{2}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 假设至少有一个钝角 | |
| B. | 假设至少有两个钝角 | |
| C. | 假设没有一个钝角 | |
| D. | 假设没有一个钝角或至少有两个钝角 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m<$\frac{17}{16}$ | B. | m>$\frac{17}{16}$ | C. | m≤$\frac{17}{16}$ | D. | m>0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com