
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\frac{{1+\sqrt{5}}}{2}$ | C. | $\frac{{-1+\sqrt{5}}}{2}$ | D. | $\frac{5}{2}$ |
分析 a1=1,${a_{n+2}}=\frac{1}{{{a_n}+1}}$,可得a3=$\frac{1}{{a}_{1}+1}$.由于a100=a96,${a}_{100}=\frac{1}{{a}_{98}+1}$,a98=$\frac{1}{{a}_{96}+1}$,化为${a}_{100}=\frac{{a}_{100}+1}{{a}_{100}+2}$,an>0,解得${a}_{100}=\frac{\sqrt{5}-1}{2}$,可得a100=a1004=…=a100+4×479=a2016,即可得出.
解答 解:∵a1=1,${a_{n+2}}=\frac{1}{{{a_n}+1}}$,∴a3=$\frac{1}{{a}_{1}+1}$=$\frac{1}{2}$.
∵a100=a96,${a}_{100}=\frac{1}{{a}_{98}+1}$,a98=$\frac{1}{{a}_{96}+1}$,化为${a}_{100}=\frac{{a}_{96}+1}{{a}_{96}+2}$,即${a}_{100}=\frac{{a}_{100}+1}{{a}_{100}+2}$,an>0,解得${a}_{100}=\frac{\sqrt{5}-1}{2}$,
∴a100=a1004=…=a100+4×479=a2016=$\frac{\sqrt{5}-1}{2}$.
∴a2016+a3=$\frac{\sqrt{5}}{2}$.
故选:A.
点评 本题考查了递推关系的应用、数列的周期性,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | y=x2+4x+7 | B. | y=x2+4x+1 | C. | y=x2-4x+7 | D. | y=x2-4x-7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 47 | B. | 48 | C. | 54 | D. | 55 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | 3 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a1+a101>0 | B. | a2+a100<0 | C. | a3+a99=0 | D. | a51=51 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
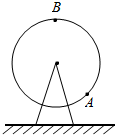 乐场有一个按逆时针方向旋转的大风车,如图所示.已知某人从点A处上风车,离地面的高度h(米)与它登上大风车后运行的时间t(分钟)满足函数关系h=12.5+10cos($\frac{2π}{15}$t-$\frac{2π}{3}$),且5分钟后到达顶点B.
乐场有一个按逆时针方向旋转的大风车,如图所示.已知某人从点A处上风车,离地面的高度h(米)与它登上大风车后运行的时间t(分钟)满足函数关系h=12.5+10cos($\frac{2π}{15}$t-$\frac{2π}{3}$),且5分钟后到达顶点B.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{9}{4}$ | C. | 9 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com