
【题目】求经过点![]() 且分别满足下列条件的直线的一般式方程.
且分别满足下列条件的直线的一般式方程.
(1)倾斜角为45°;
(2)在![]() 轴上的截距为5;
轴上的截距为5;
(3)在第二象限与坐标轴围成的三角形面积为4.
科目:高中数学 来源: 题型:
【题目】现在很多人喜欢自助游,2017年孝感杨店桃花节,美丽的桃花风景和人文景观迎来众多宾客.某调查机构为了了解“自助游”是否与性别有关,在孝感桃花节期间,随机抽取了![]() 人,得如下所示的列联表:
人,得如下所示的列联表:
赞成“自助游” | 不赞成“自助游” | 合计 | |
男性 |
| ||
女性 |
| ||
合计 |
|
(1)若在![]() 这人中,按性别分层抽取一个容量为
这人中,按性别分层抽取一个容量为![]() 的样本,女性应抽
的样本,女性应抽![]() 人,请将上面的列联表补充完整,并据此资料能否在犯错误的概率不超过
人,请将上面的列联表补充完整,并据此资料能否在犯错误的概率不超过![]() 前提下,认为赞成“自助游”是与性别有关系?
前提下,认为赞成“自助游”是与性别有关系?
(2)若以抽取样本的频率为概率,从旅游节大量游客中随机抽取![]() 人赠送精美纪念品,记这
人赠送精美纪念品,记这![]() 人中赞成“自助游”人数为
人中赞成“自助游”人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附: 
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某篮球队对篮球运动员的篮球技能进行统计研究,针对篮球运动员在投篮命中时,运动员在篮筐中心的水平距离这项指标,对某运动员进行了若干场次的统计,依据统计结果绘制如下频率分布直方图:
(Ⅰ)依据频率分布直方图估算该运动员投篮命中时,他到篮筐中心的水平距离的中位数;
(Ⅱ)在某场比赛中,考察他前4次投篮命中到篮筐中心的水平距离的情况,并且规定:运动员投篮命中时,他到篮筐中心的水平距离不少于4米的记1分,否则扣掉1分.用随机变量X表示第4次投篮后的总分,将频率视为概率,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,过点P分别做圆O的切线PA、PB和割线PCD,弦BE交CD于F,满足P、B、F、A四点共圆.
(Ⅰ)证明:AE∥CD;
(Ⅱ)若圆O的半径为5,且PC=CF=FD=3,求四边形PBFA的外接圆的半径.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 截以坐标原点
截以坐标原点![]() 为圆心的圆所得的弦长为
为圆心的圆所得的弦长为![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)若直线![]() 与圆
与圆![]() 切于第一象限,且与坐标轴交于点
切于第一象限,且与坐标轴交于点![]() ,
,![]() ,当
,当![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(3)设![]() ,
,![]() 是圆
是圆![]() 上任意两点,点
上任意两点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,若直线
,若直线![]() ,
,![]() 分别交
分别交![]() 轴于点
轴于点![]() 和
和![]() ,问
,问![]() 是否为定值?若是,请求出该定值;若不是,请说明理由.
是否为定值?若是,请求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某篮球队对篮球运动员的篮球技能进行统计研究,针对篮球运动员在投篮命中时,运动员在篮筐中心的水平距离这项指标,对某运动员进行了若干场次的统计,依据统计结果绘制如下频率分布直方图:
(Ⅰ)依据频率分布直方图估算该运动员投篮命中时,他到篮筐中心的水平距离的中位数;
(Ⅱ)在某场比赛中,考察他前4次投篮命中到篮筐中心的水平距离的情况,并且规定:运动员投篮命中时,他到篮筐中心的水平距离不少于4米的记1分,否则扣掉1分.用随机变量X表示第4次投篮后的总分,将频率视为概率,求X的分布列和数学期望.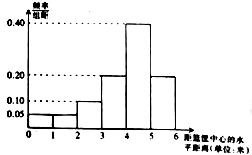
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在2019迎新年联欢会上,为了活跃大家气氛,设置了“摸球中奖”游戏,桌子上放置一个不透明的箱子,箱子中有3个黄色、3个白色的乒乓球(其体积、质地完全相同)游戏规则:从箱子中随机摸出3个球,若摸得同一颜色的3个球,摸球者中奖价值50元奖品;若摸得非同一颜色的3个球,摸球者中奖价值20元奖品.
(1)摸出的3个球为白球的概率是多少?
(2)假定有10人次参与游戏,试从概率的角度估算一下需要准备多少元钱购买奖品?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com