
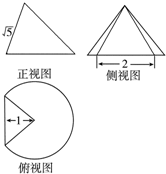
 一个圆锥被过顶点的平面截去了较小的一部分,余下的几何体的三视图如图,则该几何体的表面积为( )
一个圆锥被过顶点的平面截去了较小的一部分,余下的几何体的三视图如图,则该几何体的表面积为( )| A. | $\sqrt{5}$+$\frac{3\sqrt{3}π}{2}$+$\frac{3π}{2}$+1 | B. | 2$\sqrt{5}$+3$\sqrt{3}$π+$\frac{3π}{2}$+1 | C. | $\sqrt{5}$+$\frac{3\sqrt{3}π}{2}$+$\frac{3π}{2}$ | D. | $\sqrt{5}$+$\frac{3\sqrt{3}π}{2}$+$\frac{π}{2}$+1 |
分析 由三视图求出圆锥母线,高,底面半径.余下部分的几何体的表面积应为剩余的圆锥侧面,圆锥底面,截面三角形三部分面积之和.
解答 解:由三视图求得,圆锥母线l=$\sqrt{5+1}$=$\sqrt{6}$,圆锥的高h=$\sqrt{5-1}$=2,圆锥底面半径为r=$\sqrt{6-4}$=$\sqrt{2}$,
截去的底面弧的圆心角为直角,截去的弧长是底面圆周的$\frac{1}{4}$,圆锥侧面剩余$\frac{3}{4}$,
S1=$\frac{3}{4}$πrl=$\frac{3}{4}π×\sqrt{2}×\sqrt{6}$=$\frac{3\sqrt{3}}{2}π$
底面剩余部分为S2=$\frac{3}{4}π{r}^{2}+\frac{1}{2}×\sqrt{2}×\sqrt{2}$=$\frac{3π}{2}$+1
另外截面三角形面积为S3=$\frac{1}{2}×2×\sqrt{5}$=$\sqrt{5}$
所以余下部分的几何体的表面积为S1+S2+S3=$\frac{3\sqrt{3}}{2}π$+$\frac{3π}{2}$+1+$\sqrt{5}$.
故选A
点评 本题考查几何体表面积计算.本题关键是弄清几何体的结构特征及表面构成情况,也是易错之处.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | -$\frac{1}{5}$ | C. | $\frac{7}{5}$ | D. | -$\frac{7}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a2c>b2c(c∈R) | B. | $\frac{b}{a}>1$ | C. | lg(a-b)>0 | D. | ${({\frac{1}{2}})^a}>{({\frac{1}{2}})^b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{2}$ | B. | $\frac{3\sqrt{2}}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{9}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
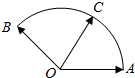 给定两个长度为1的平面向量$\overrightarrow{OA}$和$\overrightarrow{OB}$,它们的夹角为120°.点C在以OA,OB为半径的圆弧上,∠AOC=30°如图所示,若$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,其中x,y∈R,则x=$\frac{2\sqrt{3}}{3}$;y=$\frac{\sqrt{3}}{3}$.
给定两个长度为1的平面向量$\overrightarrow{OA}$和$\overrightarrow{OB}$,它们的夹角为120°.点C在以OA,OB为半径的圆弧上,∠AOC=30°如图所示,若$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,其中x,y∈R,则x=$\frac{2\sqrt{3}}{3}$;y=$\frac{\sqrt{3}}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com