
分析 f(x)解析式提取,利用两角和与差的正弦函数公式化为一个角的正弦函数,由x=θ时,函数f(x)取得最大值,得到sinθ-2cosθ=$\sqrt{5}$,与sin2θ+cos2θ=1联立即可求出cosθ的值和sinθ的值,即可求出答案
解答 解:f(x)=sinx-2cosx=$\sqrt{5}$($\frac{\sqrt{5}}{5}$sinx-$\frac{2\sqrt{5}}{5}$cosx)=$\sqrt{5}$sin(x-α)(其中cosα=$\frac{\sqrt{5}}{5}$,sinα=$\frac{2\sqrt{5}}{5}$),
∵x=θ时,函数f(x)取得最大值,
∴sin(θ-α)=1,即sinθ-2cosθ=$\sqrt{5}$>0,
又sin2θ+cos2θ=1,
联立得(2cosθ+$\sqrt{5}$)2+cos2θ=1,解得cosθ=-$\frac{2\sqrt{5}}{5}$,
∴sinθ=$\frac{\sqrt{5}}{5}$,
∴tanθ=$-\frac{1}{2}$,
故答案为:-$\frac{1}{2}$.
点评 此题考查了两角和与差的正弦函数公式,同角三角函数间的基本关系,以及正弦函数的定义域与值域,熟练掌握公式是解本题的关键.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:选择题
| A. | [kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$](k∈Z) | B. | [kπ,kπ+$\frac{π}{2}$](k∈Z) | C. | [kπ+$\frac{π}{6}$,kπ+$\frac{2π}{3}$](k∈Z) | D. | [kπ-$\frac{π}{2}$,kπ](k∈Z) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
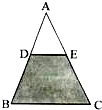 如图所示,已知D、E分别是△ABC的边AB、AC的中点,把一粒黄豆随机投到△ABC内,则黄豆落到阴影区域内的概率是( )
如图所示,已知D、E分别是△ABC的边AB、AC的中点,把一粒黄豆随机投到△ABC内,则黄豆落到阴影区域内的概率是( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
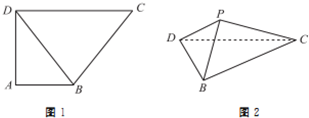 已知直角梯形ABCD中,AB∥CD,AB⊥AD,CD=2,AD=$\sqrt{2}$,AB=1,如图1所示,将△ABD沿BD折起到△PBD的位置,如图2所示.
已知直角梯形ABCD中,AB∥CD,AB⊥AD,CD=2,AD=$\sqrt{2}$,AB=1,如图1所示,将△ABD沿BD折起到△PBD的位置,如图2所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 解方程2x-6=0的过程是移项和系数化为1 | |
| B. | 从济南到温哥华要先乘火车到北京,再转乘飞机 | |
| C. | 解方程2x2+x-1=0 | |
| D. | 利用公式S=πγ2计算半径为3的圆的面积是计算π×32 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\sqrt{3}$,4) | B. | ($\sqrt{2}$,+∞) | C. | ($\sqrt{2}$,5) | D. | ($\sqrt{3}$,2$\sqrt{2}$ ) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com