考点:二面角的平面角及求法,空间中直线与直线之间的位置关系
专题:计算题,作图题,空间位置关系与距离,空间向量及应用
分析:(Ⅰ)取AB中点O,连接OM,OC,可证MO⊥AB,AB⊥CO,从而可证AB⊥平面OMC,从而可证MC⊥AB;
(Ⅱ)以O为原点,以
,
,
的方向分别为x轴,y轴,z轴的正方向,建立空间直角坐标系.如图.依题意O(0,0,0),A(-2,0,0),B(2,0,0),C(0,2
,0),M(0,0,2
),P(0,2
,
);从而求得
=(3,-
,0)为平面PAC的一个法向量,
=(0,2
,-2
)为平面PAB的一个法向量;从而求二面角B-AP-C的余弦值.
解答:
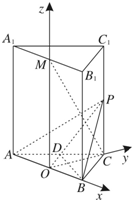
解:(I)取AB中点O,连接OM,OC.
∵M为A
1B
1中点,
∴MO∥A
1A,
又∵A
1A⊥平面ABC,
∴MO⊥平面ABC,
∴MO⊥AB;
∵△ABC为正三角形,
∴AB⊥CO,
又∵MO∩CO=O,
∴AB⊥平面OMC.
又∵MC?平面OMC,
∴AB⊥MC.
(II)以O为原点,以
,
,
的方向分别为x轴,y轴,z轴的正方向,建立空间直角坐标系.
如图.依题意O(0,0,0),A(-2,0,0),B(2,0,0),C(0,2
,0),M(0,0,2
),P(0,2
,
);
∴当P为线段CC
1的中点时,MC⊥平面ABP.
取线段AC的中点D,则D(-1,
,0),
易知DB⊥平面A
1ACC
1,
故
=(3,-
,0)为平面PAC的一个法向量.
又由(II)知
=(0,2
,-2
)为平面PAB的一个法向量.
设二面角B-AP-C的平面角为α,
则|cosα|=
=|
=
.
故二面角B-AP-C的余弦值为
.
点评:本题考查了异面直线垂直的证明,用到了线面垂直的判定与性质定理,同时考查了空间向量的应用,属于难题.

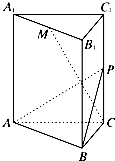 如图,三棱柱ABC-A1B1C1的底面是边长为4正三角形,AA1⊥平面ABC,AA1=2
如图,三棱柱ABC-A1B1C1的底面是边长为4正三角形,AA1⊥平面ABC,AA1=2 解:(I)取AB中点O,连接OM,OC.
解:(I)取AB中点O,连接OM,OC.
