
分析 (Ⅰ)由已知数列的前n项和求得首项,再由an=Sn-Sn-1求得n≥2时的通项公式,验证首项后得答案;
(Ⅱ)由Sn=2n2+3n-1>2n2+2n(n≥2),得$\frac{1}{{S}_{n}}<\frac{1}{2n(n+1)}=\frac{1}{2}(\frac{1}{n}-\frac{1}{n+1})$,作和后即可证明$\frac{1}{S_1}$+$\frac{1}{S_2}$+…+$\frac{1}{S_n}$<$\frac{1}{2}$.
解答 (Ⅰ)解:由Sn=2n2+3n-1,得a1=S1=4;
当n≥2时,an=Sn-Sn-1=2n2+3n-1-[2(n-1)2+3(n-1)-1]=4n+1.
当n=1时,上式不成立,
∴${a}_{n}=\left\{\begin{array}{l}{4,n=1}\\{4n+1,n≥2}\end{array}\right.$;
(Ⅱ)证明:∵2n2+3n-1-2n2-2n=n-1>0(n≥2),
∴Sn=2n2+3n-1>2n2+2n(n≥2),
则$\frac{1}{{S}_{n}}<\frac{1}{2n(n+1)}=\frac{1}{2}(\frac{1}{n}-\frac{1}{n+1})$(n≥2),
当n=1时,$\frac{1}{{S}_{1}}=\frac{1}{4}<\frac{1}{2}$成立;
当n≥2时,$\frac{1}{S_1}$+$\frac{1}{S_2}$+…+$\frac{1}{S_n}$<$\frac{1}{4}+\frac{1}{2}(\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+…+\frac{1}{n}-\frac{1}{n+1})$=$\frac{1}{4}+\frac{1}{2}(\frac{1}{2}-\frac{1}{n+1})=\frac{1}{2}-\frac{1}{2(n+1)}<\frac{1}{2}$.
∴$\frac{1}{S_1}$+$\frac{1}{S_2}$+…+$\frac{1}{S_n}$<$\frac{1}{2}$.
点评 本题考查由数列的前n项和求数列的通项公式,训练了放缩法与裂项相消法证明数列不等式,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$-1 | B. | 2$\sqrt{2}$+1 | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)是偶函数 | B. | f(x)是增函数 | C. | f(x)是周期函数 | D. | f(x)的值域为[-1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
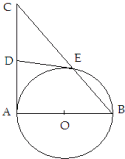 如图,AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于点E.
如图,AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于点E.查看答案和解析>>
科目:高中数学 来源:2017届湖南永州市高三高考一模考试数学(理)试卷(解析版) 题型:解答题
某届奥运会上,中国队以26金18银26铜的成绩称金牌榜第三、奖牌榜第二,某校体育爱好者在高三 年级一班至六班进行了“本届奥运会中国队表现”的满意度调查(结果只有“满意”和“不满意”两种),从被调查的学生中随机抽取了50人,具体的调查结果如下表:
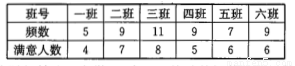
(1)在高三年级全体学生中随机抽取一名学生,由以上统计数据估计该生持满意态度的概率;
(2)若从一班至二班的调查对象中随机选取4人进行追踪调查,记选中的4人中对“本届奥运会中国队表现”不满意的人数为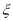 ,求随机变量
,求随机变量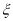 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源:2017届湖北省百所重点校高三联合考试数学(理)试卷(解析版) 题型:解答题
已知函数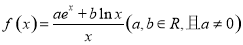 .
.
(1)若曲线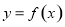 在点
在点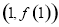 处的切线与
处的切线与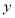 轴垂直,且
轴垂直,且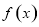 有极大值,求实数
有极大值,求实数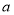 的取值范围;
的取值范围;
(2)若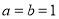 ,试判断
,试判断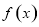 在
在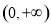 上的单调性,并加以证明.(提示:
上的单调性,并加以证明.(提示: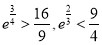 ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com