
分析 (1)求出函数的导数,求出a的值,解关于导函数的不等式,求出函数的单调区间,从而求出函数的极值即可;
(2)令$φ(x)=\frac{e^x}{{f(x)-{x^3}}}=\frac{e^x}{{{x^2}-x+1}}$,通过求导得到函数的单调性,通过讨论x的范围证出结论即可.
解答 解:(1)依题意,f'(x)=3x2+2x-a,f'(1)=3+2-a=4,a=1,
故f'(x)=3x2+2x-1=(3x-1)(x+1),
令f'(x)>0,则x<-1或$x>\frac{1}{3}$; 令f'(x)<0,则$-1<x<\frac{1}{3}$,
故当x=-1时,函数f(x)有极大值f(-1)=2,
当$x=\frac{1}{3}$时,函数f(x)有极小值$f({\frac{1}{3}})=\frac{22}{27}$…(5分)
证明:(2)由(1)知a=1,令$φ(x)=\frac{e^x}{{f(x)-{x^3}}}=\frac{e^x}{{{x^2}-x+1}}$,
则$φ'(x)=\frac{{{e^x}({{x^2}-x+1})-({2x-1}){e^x}}}{{{{({{x^2}-x+1})}^2}}}=\frac{{{e^x}({x-1})({x-2})}}{{{{({{x^2}-x+1})}^2}}}$,
可知φ(x)在(0,1)上单调递增,在(1,2)上单调递减,令g(x)=x.
①当x∈[0,1]时,φ(x)min=φ(0)=1,g(x)max=1,
所以函数φ(x)的图象在g(x)图象的上方.
②当x∈[1,2]时,函数φ(x)单调递减,
所以其最小值为$φ(2)=\frac{e^2}{3},g(x)$最大值为2,而$\frac{e^2}{3}>2$,
所以函数φ(x)的图象也在g(x)图象的上方.
综上可知,当0≤x≤a+1时,$\frac{e^x}{{f(x)-{x^3}}}>x$…(12分)
点评 本题考查了函数的单调性、极值问题,考查导数的应用以及不等式的证明,是一道中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{2}$ | B. | 2 | C. | $\sqrt{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届湖南永州市高三高考一模考试数学(理)试卷(解析版) 题型:解答题
选修4-5:不等式选讲
已知函数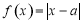 .
.
(Ⅰ)若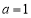 ,解不等式:
,解不等式: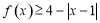 ;
;
(Ⅱ)若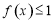 的解集为
的解集为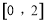 ,
,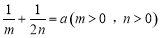 ,求
,求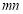 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源:2017届湖北省百所重点校高三联合考试数学(文)试卷(解析版) 题型:选择题
为得到函数 的图象,可将函数
的图象,可将函数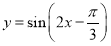 的图象( )
的图象( )
A.向左平移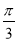 个单位 B.向左平移
个单位 B.向左平移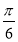 个单位
个单位
C.向右平移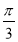 个单位 D.向右平移
个单位 D.向右平移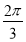 个单位
个单位
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com