
分析 根据余弦定理,算出(b+c)2=16+3bc,再利用基本不等式,加以计算,可得b+c≤8,即可得到△ABC周长的最大值.
解答 解:∵在△ABC中,A=60°,a=4,
∴由余弦定理,得a2=b2+c2-2bccosA,
即16=b2+c2-2bccos60°=b2+c2-bc≥2bc-bc=bc(当且仅当b=c时等号成立),
∵16=b2+c2-bc=(b+c)2-3bc,
∴(b+c)2≤16+3bc≤16+3×16=64,由此可得b+c≤8(当且仅当b=c时等号成立),
∴△ABC周长b+c+a≤8+4=12(当且仅当b=c时等号成立),
即当且仅当b=c=4时,△ABC周长的最大值为12.
故答案为:12.
点评 本题给出三角形的一边和它的对角,求周长的最大值,着重考查了用余弦定理解三角形和基本不等式求最值等知识,属于中档题.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
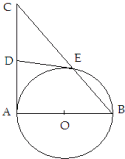 如图,AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于点E.
如图,AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于点E.查看答案和解析>>
科目:高中数学 来源:2017届湖南永州市高三高考一模考试数学(理)试卷(解析版) 题型:选择题
已知函数 ,则函数
,则函数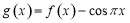 在区间
在区间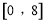 内所有零点的和为( )
内所有零点的和为( )
A.16 B.30 C.32 D.40
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com