
分析 (1)根据圆心与半径,即可求圆C的方程;
(2)直线与圆的方程联立,利用韦达定理、弦长公式,结合|AB|=2时,求斜率k的值.
解答 解:(1)由题意可知(x-2)2+(y-3)2=1;
(2)设点A(x1,y1),B(x2,y2)由(1)可知
联立方程得$\left\{\begin{array}{l}y=kx+1\\{({x-2})^2}+{({y-3})^2}=1\end{array}\right.$则有(1+k2)x2-4(1+k)x+7=0,△=-3k2+8k-3>0
所以 ${x_1}+{x_2}=\frac{{4({1+k})}}{{1+{k^2}}}$①${x_1}•{x_2}=\frac{7}{{1+{k^2}}}$②
因为|AB|=2
所以$\sqrt{1+{k^2}}•\sqrt{{{({{x_1}+{x_2}})}^2}-4{x_1}{x_2}}=2$③
由①②③可得 k=1.
点评 本题主要考查直线和圆的位置关系,韦达定理,弦长公式的应用,正确运用圆的性质是关键.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:选择题
| A. | (-4,-1) | B. | (-1,1) | C. | (1,2) | D. | (-4,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{2}$ | B. | 2 | C. | $\sqrt{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源:2017届湖北省百所重点校高三联合考试数学(文)试卷(解析版) 题型:解答题
已知函数 .
.
(1)若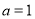 ,求函数
,求函数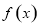 的极值和单调区间;
的极值和单调区间;
(2)若在区间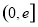 上至少存在一点
上至少存在一点 ,使得
,使得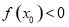 成立,求实数
成立,求实数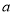 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com