
分析 (Ⅰ) 由题意可得:$\left\{\begin{array}{l}{\frac{3}{{a}^{2}}+\frac{3}{4{b}^{2}}=1}\\{\frac{c}{a}=\frac{1}{2}}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解出即可得出.
(Ⅱ)设A(x1,y1),由A是PB的中点,得B(2x1,2y1-3).把A,B坐标代入椭圆方程可得:$\left\{\begin{array}{l}\frac{x_1^2}{4}+\frac{y_1^2}{3}=1\\ \frac{{{{(2{x_1})}^2}}}{4}+\frac{{{{(2{y_1}-3)}^2}}}{3}=1\end{array}\right.$,解出即可得出.
解答 解:(Ⅰ) 由题意可得:$\left\{\begin{array}{l}{\frac{3}{{a}^{2}}+\frac{3}{4{b}^{2}}=1}\\{\frac{c}{a}=\frac{1}{2}}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得a=2,c=1,b2=3.
∴椭圆的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$.;
(Ⅱ)设A(x1,y1),由A是PB的中点,得B(2x1,2y1-3).
∵A,B在椭圆上,∴$\left\{\begin{array}{l}\frac{x_1^2}{4}+\frac{y_1^2}{3}=1\\ \frac{{{{(2{x_1})}^2}}}{4}+\frac{{{{(2{y_1}-3)}^2}}}{3}=1\end{array}\right.$,解得$\left\{\begin{array}{l}{x_1}=±1\\{y_1}=\frac{3}{2}\end{array}\right.$,
∴直线m的斜率$k=±\frac{3}{2}$.
∴直线的方程$y=±\frac{3}{2}x+3$.
点评 本题考查了椭圆的标准方程及其性质、中点坐标公式、直线的方程,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | (0,2) | B. | (-∞,0] | C. | [1,+∞) | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 17 | C. | 26 | D. | 2016 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
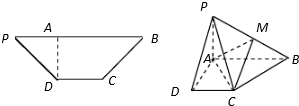 已知等腰梯形PDCB中,PB=3,DC=1,PD=BC=$\sqrt{2}$,A为PB边上一点,且PA=1,将△PAD沿AD折起,使平面PAD⊥平面ABCD.
已知等腰梯形PDCB中,PB=3,DC=1,PD=BC=$\sqrt{2}$,A为PB边上一点,且PA=1,将△PAD沿AD折起,使平面PAD⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com