Question

12．由函数y=lgx的图象画出下列函数的图象．
（1）y=lg（x-1）；
（2）y=lg|x|；
（3）y=|lgx-1|；
（4）y=lg|x-1|

Answer 1

分析 （1）由函数y=lgx的图象向右平移1个单位得到y=lg（x-1）的图象；
（2）由函数y=lgx的图象保留y轴右边的图象，再翻折到y轴的左边得到y=lg|x|的图象；
（3）由函数y=lgx的图象向下平移1个单位得到y=lgx-1的图象，再将y轴上方保留，下方翻折到x轴上方，得到y=|lgx-1|的图象；
（4）由函数y=lgx的图象保留y轴右边的图象，再翻折到y轴的左边得到y=lg|x|的图象，再向右平移1个单位得到y=lg|x-1|的图象．

解答 解：（1）由函数y=lgx的图象向右平移1个单位得到y=lg（x-1）的图象；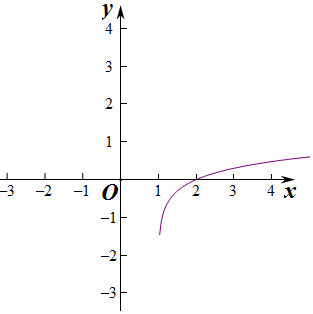

（2）由函数y=lgx的图象保留y轴右边的图象，再翻折到y轴的左边得到y=lg|x|的图象；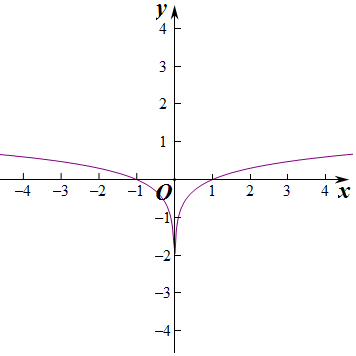

（3）由函数y=lgx的图象向下平移1个单位得到y=lgx-1的图象，再将y轴上方保留，下方翻折到x轴上方，得到y=|lgx-1|的图象；

（4）由函数y=lgx的图象保留y轴右边的图象，再翻折到y轴的左边得到y=lg|x|的图象，再向右平移1个单位得到y=lg|x-1|的图象．

点评 本题考查利用图象变换做函数的图象，考查学生的作图能力，正确运用图象变换是关键．