
分析 由两圆的方程分别找出圆心M与N的坐标,及两圆的半径r1与r2,设圆P的半径为r,根据圆P与M外切,与B内切,得到PM=r+2,PN=r-2,即可可得出轨迹方程.
解答 解:由圆$M:{({x+\sqrt{5}})^2}+{y^2}$=4,圆$N:{({x-\sqrt{5}})^2}+{y^2}$=4,
得到M(-$\sqrt{5}$,0),半径r1=2,N($\sqrt{5}$,0),半径r2=2,
设圆P的半径为r,
∵与圆M外切而内切于圆N,
∴PM=r+2,PN=r-2,
∴PM-PN=4,又MN=2c=2$\sqrt{5}$,
∴P的轨迹是双曲线的右支,a=2,c=$\sqrt{5}$,
∴b=1,
∴圆心P的轨迹方程$\frac{x^2}{4}-{y^2}=1,({x≥2})$.
故答案为$\frac{x^2}{4}-{y^2}=1,({x≥2})$.
点评 此题考查了圆与圆的位置关系,双曲线的基本性质,以及动点的轨迹方程,两圆的位置关系由圆心角d与两圆半径R,r的关系来判断,当d<R-r时,两圆内含;当d=R-r时,两圆内切;当R-r<d<R+r时,两圆相交;当d=R+r时,两圆外切;当d>R+r时,两圆外离.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 17 | C. | 26 | D. | 2016 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3\sqrt{10}}{10}$ | B. | $\frac{\sqrt{10}}{10}$ | C. | $\frac{1}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -36 | B. | -34 | C. | -36-$\frac{1}{{2}^{5}}$ | D. | -34-$\frac{1}{{2}^{5}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
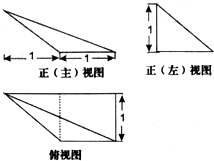
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com