
分析 (1)求出二次函数的对称轴方程,然后分类得到函数在[0,1]上的单调性,由单调性求得最小值;
(2)直接分类由最小值为$\frac{1}{2}$解得a的值.
解答 解:(1)函数f(x)=x2-ax+1的对称轴方程为x=$\frac{a}{2}$,
当$\frac{a}{2}≤0$,即a≤0时,g(a)=f(0)=1.
当$\frac{a}{2}≥1$,即a≥2时,g(a)=f(1)=2-a.
当0$<\frac{a}{2}<1$,即0<a<2时,g(a)=f($\frac{a}{2}$)=1-$\frac{{a}^{2}}{4}$.
∴$g(a)=\left\{\begin{array}{l}{1,a≤0}\\{1-\frac{{a}^{2}}{4},0<a<2}\\{2-a,a≥2}\end{array}\right.$;
(2)由$1-\frac{{a}^{2}}{4}=\frac{1}{2}$,解得:a=$±\sqrt{2}$,∵0<a<2,∴a=$\sqrt{2}$.
由2-a=$\frac{1}{2}$,解得a=$\frac{3}{2}$(舍).
∴若该函数最小值为$\frac{1}{2}$,则a=$\sqrt{2}$.
点评 本题考查二次函数在闭区间上的最值,考查了分类讨论的数学思想方法,是基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
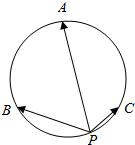 如图,A,B,C是圆O上的三等分点,点P在劣弧$\widehat{BC}$上,且PB=2,PC=1,若实数x,y,z满足x$\overrightarrow{PA}$+y$\overrightarrow{PB}$+z$\overrightarrow{PC}$=$\overrightarrow{0}$.则x:y:z=( )
如图,A,B,C是圆O上的三等分点,点P在劣弧$\widehat{BC}$上,且PB=2,PC=1,若实数x,y,z满足x$\overrightarrow{PA}$+y$\overrightarrow{PB}$+z$\overrightarrow{PC}$=$\overrightarrow{0}$.则x:y:z=( )| A. | (-1):2:3 | B. | (-3):2:1 | C. | (-2):3:6 | D. | (-6):3:2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com