
【题目】已知函数![]() ,若存在
,若存在![]() ,使得
,使得![]() ,则实数
,则实数![]() 的值为______.
的值为______.
【答案】![]()
【解析】
函数f(x)可以看作是动点M(x,ex)与动点N(-a,-![]() )之间距离的平方,问题转化为求直线上的动点到曲线的最小距离,由y=ex得,y′=ex=
)之间距离的平方,问题转化为求直线上的动点到曲线的最小距离,由y=ex得,y′=ex=![]() ,曲线上点M(-1,
,曲线上点M(-1,![]() )到直线y=
)到直线y=![]() x的距离最小,要使f(x0)≤
x的距离最小,要使f(x0)≤![]() ,则f(x0)=
,则f(x0)=![]() ,然后求解a即可.
,然后求解a即可.
函数f(x)=(x+a)2+(ex+![]() )2,
)2,
函数f(x)可以看作是动点M(x,ex)与动点N(-a,-![]() )之间距离的平方,
)之间距离的平方,
动点M在函数y=ex的图象上,N在直线y=![]() x的图象上,
x的图象上,
问题转化为求直线上的动点到曲线的最小距离,
由y=ex得,y′=ex=![]() ,解得x=-1,
,解得x=-1,
所以曲线上点M(-1,![]() )到直线y=
)到直线y=![]() x的距离最小,最小距离d=
x的距离最小,最小距离d=![]() ,
,
则f(x)≥![]() ,
,
根据题意,要使f(x0)≤![]() ,则f(x0)=
,则f(x0)=![]() ,
,
此时N恰好为垂足,由KMN=-e,解得a=![]() .
.
故答案为:![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的焦点是椭圆
的焦点是椭圆![]() :
: ![]() (
(![]() )的顶点,且椭圆与双曲线的离心率互为倒数.
)的顶点,且椭圆与双曲线的离心率互为倒数.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设动点![]() ,
, ![]() 在椭圆
在椭圆![]() 上,且
上,且![]() ,记直线
,记直线![]() 在
在![]() 轴上的截距为
轴上的截距为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为更好地落实农民工工资保证金制度,南方某市劳动保障部门调查了![]() 年下半年该市
年下半年该市![]() 名农民工(其中技术工、非技术工各
名农民工(其中技术工、非技术工各![]() 名)的月工资,得到这
名)的月工资,得到这![]() 名农民工月工资的中位数为
名农民工月工资的中位数为![]() 百元(假设这
百元(假设这![]() 名农民工的月工资均在
名农民工的月工资均在![]() (百元)内)且月工资收入在
(百元)内)且月工资收入在![]() (百元)内的人数为
(百元)内的人数为![]() ,并根据调查结果画出如图所示的频率分布直方图:
,并根据调查结果画出如图所示的频率分布直方图:

(Ⅰ)求![]() ,
,![]() 的值;
的值;
(Ⅱ)已知这![]() 名农民工中月工资高于平均数的技术工有
名农民工中月工资高于平均数的技术工有![]() 名,非技术工有
名,非技术工有![]() 名,则能否在犯错误的概率不超过
名,则能否在犯错误的概率不超过![]() 的前提下认为是不是技术工与月工资是否高于平均数有关系?
的前提下认为是不是技术工与月工资是否高于平均数有关系?
参考公式及数据: ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
在直角坐标系![]() 中,点P到两点
中,点P到两点![]() ,
,![]() 的距离之和等于4,设点P的轨迹为
的距离之和等于4,设点P的轨迹为![]() ,直线
,直线![]() 与C交于A,B两点.
与C交于A,B两点.
(Ⅰ)写出C的方程;
(Ⅱ)若![]()
![]()
![]() ,求k的值;
,求k的值;
(Ⅲ)若点A在第一象限,证明:当k>0时,恒有|![]() |>|
|>|![]() |.
|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】1927年德国汉堡大学的学生考拉兹提出一个猜想:对于每一个正整数,如果它是奇数,就把它乘以3再加1,如果它是偶数,就把它除以2,这样循环,最终结果都能得到1.如图是为了验证考拉兹猜想而设计的一个程序框图,则①处应填写的条件及输出的结果i分别为( )
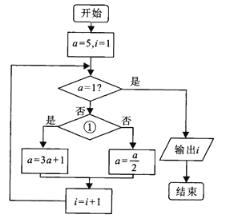
A.a是偶数?;5B.a是偶数?;6
C.a是奇数?;5D.a是奇数?;6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用长为18 cm的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为2:1,问该长方体的长、宽、高各为多少时,其体积最大?最大体积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 及点
及点![]() ,
,![]() .
.
(1)若直线![]() 平行于
平行于![]() ,与圆
,与圆![]() 相交于
相交于![]() ,
,![]() 两点,
两点,![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)在圆![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求点
?若存在,求点![]() 的个数;若不存在,说明理由.
的个数;若不存在,说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com