
分析 (1)求出方程f(x)=0的根,利用配方法化简后,由二次函数的图象画出f(x)的函数图象,由图象写出f(x)的单调区间;
(2)将函数g(x)的零点问题转化为函数图象的交点问题,由图求出m的取值范围.
解答 解:(1)令f(x)=|x2-2x-3|=0,解得x=-1或x=3,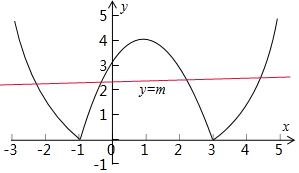
画出函数f(x)=|x2-2x-3|=|(x-1)2-4|的图象:
由图得,
f(x)的增区间是(-1,1),(3,+∞),
减区间是(-∞,-1),(1,3);
(2)∵g(x)=f(x)-m有4个零点,
∴函数y=f(x)的图象与直线y=m有4个不同的交点,
由图得,m的取值范围是(0,4).
点评 本题考查了函数的零点与函数图象的交点关系,以及二次函数的图象,考查转化思想、数形结合思想,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2)∪[2,+∞) | B. | (-2,2) | C. | (-2,2] | D. | (-∞,2] |
查看答案和解析>>
科目:高中数学 来源:2017届湖南永州市高三高考一模考试数学(文)试卷(解析版) 题型:选择题
某学校高一、高二、高三年级的学生人数之比为4:3:3,现用分层抽样的方法从该校高中三个年级的学生中抽取容量为50的样本,则从高二年级抽取的学生人数为( )
A.15 B.20 C.25 D.30
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在三棱锥S-ABC中,∠SAB=∠SAC=∠ACB=90°,且AC=BC=5,SB=$5\sqrt{5}$.(如图所示)
在三棱锥S-ABC中,∠SAB=∠SAC=∠ACB=90°,且AC=BC=5,SB=$5\sqrt{5}$.(如图所示)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com