
| A. | (-∞,-2)∪[2,+∞) | B. | (-2,2) | C. | (-2,2] | D. | (-∞,2] |
分析 根据题意,讨论m的取值范围,求出使不等式恒成立的m的取值范围即可.
解答 解:∵不等式mx2+2mx-4<2x2+4x对任意实数x均成立,
∴(m-2)x2+2(m-2)x-4<0,
当m-2=0,即m=2时,不等式为-4<0,显然成立;
当m-2≠0,即m≠2时,应满足$\left\{\begin{array}{l}{m-2<0}\\{△=4(m-2)^{2}+16(m-2)<0}\end{array}\right.$,
解得-2<m<2;
综上,-2<m≤2,
即实数m的取值范围是(-2,2].
故选:C.
点评 本题考查了不等式的恒成立问题,解题时应对字母系数进行讨论,是中档题.


科目:高中数学 来源:2017届湖南永州市高三高考一模考试数学(文)试卷(解析版) 题型:解答题
选修4-1:几何证明选讲
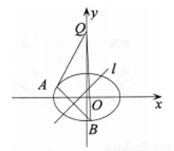
如图,圆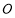 是
是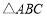 的外接圆,
的外接圆,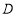 是
是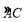 的中点,
的中点,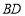 交
交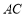 于
于 .
.
(Ⅰ)求证: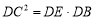 ;
;
(Ⅱ)若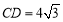 ,点
,点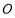 到
到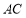 的距离等于点
的距离等于点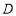 到
到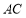 的距离的一半,求圆
的距离的一半,求圆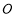 的半径
的半径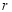 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{-\sqrt{7}}{2}$,$\frac{\sqrt{3}}{2}$) | B. | ($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$) | C. | ($\frac{-1}{2}$,$\frac{1}{2}$) | D. | ($\frac{-1+\sqrt{7}}{2}$,$\frac{1+\sqrt{3}}{2}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com