
(本题满分18分)在平面直角坐标系中,已知动点 ,点
,点 点
点 与点
与点 关于直线
关于直线 对称,且
对称,且 .直线
.直线 是过点
是过点 的任意一条直线.
的任意一条直线.
(1)求动点 所在曲线
所在曲线 的轨迹方程;
的轨迹方程;
(2)设直线 与曲线
与曲线 交于
交于 两点,且
两点,且 ,求直线
,求直线 的方程;
的方程;
(3) 设直线 与曲线
与曲线 交于
交于 两点,求以
两点,求以 的长为直径且经过坐标原点
的长为直径且经过坐标原点 的圆的方程.
的圆的方程.
(1) 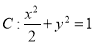 ; (2)
; (2) 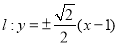 ; (3)
; (3) 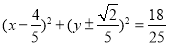 .
.
【解析】
试题分析:(1)求出N的坐标,运用向量的数量积的坐标表示,化简即可得到轨迹方程;
(2)设l:y=k(x-1),联立椭圆方程,消去y,运用韦达定理和弦长公式,即可求得斜率,进而得到直线方程;
(3)由于当直线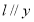 轴时,
轴时,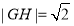 ,点
,点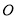 到圆心的距离为1.即点
到圆心的距离为1.即点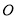 在圆外,不满足题意.所以满足题意的直线
在圆外,不满足题意.所以满足题意的直线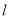 的斜率存在,设为
的斜率存在,设为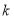 ,则
,则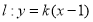 ,由(2)可得
,由(2)可得 ,由点O在圆上知:
,由点O在圆上知: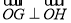 ,从而由向量的数量积可求出k的值,进而就可求出半径和圆心坐标,所以就可写出圆的方程.
,从而由向量的数量积可求出k的值,进而就可求出半径和圆心坐标,所以就可写出圆的方程.
试题解析:(1)依据题意,可得点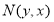 .
.
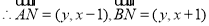 .
.
又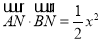 ,
,
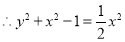 .
.
 所求动点
所求动点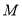 的轨迹方程为
的轨迹方程为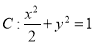 .
.
(2) 若直线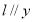 轴,则可求得
轴,则可求得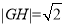 ,这与已知矛盾,因此满足题意的直线
,这与已知矛盾,因此满足题意的直线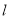 不平行于
不平行于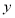 轴.
轴.
设直线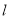 的斜率为
的斜率为 ,则
,则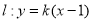 .
.
由 得
得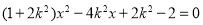 .
.
设点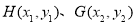 ,有
,有 且
且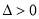 恒成立(因点
恒成立(因点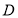 在椭圆内部).
在椭圆内部).
又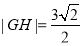 ,
,
于是, ,即
,即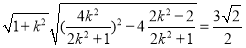 ,
,
解得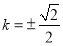 .
.
所以,所求直线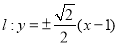 .
.
(3)  当直线
当直线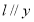 轴时,
轴时,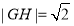 ,点
,点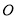 到圆心的距离为1.即点
到圆心的距离为1.即点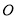 在圆外,不满足题意.
在圆外,不满足题意.
 满足题意的直线
满足题意的直线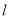 的斜率存在,设为
的斜率存在,设为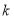 ,则
,则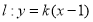 .
.
设点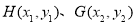 ,由(2)知,
,由(2)知, 进一步可求得
进一步可求得
依据题意,有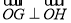 ,
,
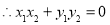 ,
,
即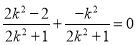 ,解得
,解得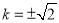 .
.
 所求圆的半径
所求圆的半径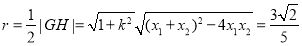 ,
,
圆心为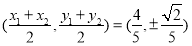 .
.
 所求圆的方程为:
所求圆的方程为: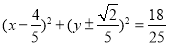 .
.
考点:直线与圆锥曲线的综合问题.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源:[同步]2014年北师大版选修2-1 2.5夹角的计算练习卷(解析版) 题型:?????
若平面α的法向量为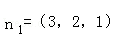 ,平面β的法向量为
,平面β的法向量为 ,则平面α与β夹角(锐角)的余弦是( )
,则平面α与β夹角(锐角)的余弦是( )
A.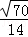 B.
B.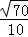 C.
C.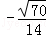 D.﹣
D.﹣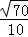
查看答案和解析>>
科目:高中数学 来源:2014-2015学年四川省成都市高三第一次诊断性检测文科数学试卷(解析版) 题型:选择题
已知抛物线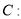
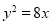 ,过点
,过点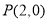 的直线与抛物线交于
的直线与抛物线交于 ,
,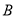 两点,
两点,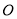 为坐标原点,则
为坐标原点,则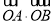 的值为
的值为
(A)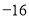 (B)
(B)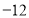 (C)
(C)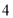 (D)
(D)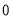
查看答案和解析>>
科目:高中数学 来源:2014-2015学年四川省成都市高三第一次诊断性检测理科数学试卷(解析版) 题型:填空题
二项式 的展开式中含
的展开式中含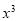 的项的系数是__________.(用数字作答)
的项的系数是__________.(用数字作答)
查看答案和解析>>
科目:高中数学 来源:2014-2015学年四川省成都市高三第一次诊断性检测理科数学试卷(解析版) 题型:选择题
已知命题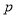 :“若
:“若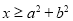 ,则
,则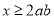 ”,则下列说法正确的是( )
”,则下列说法正确的是( )
(A)命题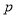 的逆命题是“若
的逆命题是“若 ,则
,则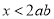 ”
”
(B)命题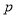 的逆命题是“若
的逆命题是“若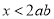 ,则
,则 ”
”
(C)命题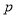 的否命题是“若
的否命题是“若 ,则
,则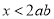 ”
”
(D)命题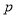 的否命题是“若
的否命题是“若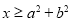 ,则
,则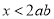 ”
”
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上海市黄浦区高三上学期期终调研测试文科数学试卷(解析版) 题型:选择题
已知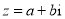
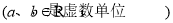 ,
,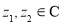 ,定义:
,定义: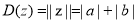 ,
,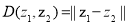 .给出下列命题:
.给出下列命题:
(1)对任意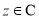 ,都有
,都有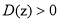 ;
;
(2)若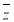 是复数
是复数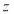 的共轭复数,则
的共轭复数,则 恒成立;
恒成立;
(3)若
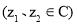 ,则
,则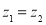 ;
;
(4)对任意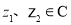 ,结论
,结论 恒成立,则其中真命题是( ).
恒成立,则其中真命题是( ).
A.(1)(2)(3)(4) B.(2)(3)(4) C.(2)(4) D.(2)(3)
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上海市黄浦区高三上学期期终调研测试文科数学试卷(解析版) 题型:填空题
已知 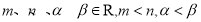 ,若
,若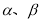 是函数
是函数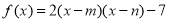 的零点,则
的零点,则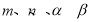 四个数按从小到大的顺序是 (用符号
四个数按从小到大的顺序是 (用符号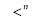 连接起来).
连接起来).
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上海市黄浦区高三上学期期终调研测试理科数学试卷(解析版) 题型:选择题
一个算法的程序框图如图所示,则该程序运行后输出的值是( ).
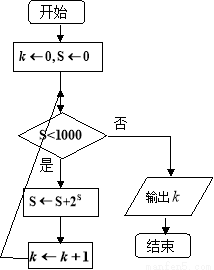
A.4 B. 5 C. 6 D. 7
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省莱州市高三上学期期末考试理科数学试卷(解析版) 题型:选择题
某次数学摸底考试共有10道选择题,每道题四个选项中有且只有一个选项是正确的;张三同学每道题都随意地从中选了一个答案,记该同学至少答对9道题的概率为P,则下列数据中与P的值最接近的是
A.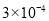 B.
B. C.
C.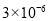 D.
D.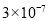
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com