
分析 (1)根据分式的性质,利用分子常数化,转化为基本不等式进行求解即可.
(2)将分式不等式转化为一元二次不等式,讨论参数b的取值范围进行求解即可.
解答 解:(1)∵当a=1,b=2时,f(x)=$\frac{{x}^{2}+3x-3}{x-1}$=x-1+$\frac{1}{x-1}$+5,(x≠1) (1分)
?当x>1时,即x-1>0.
∴f(x)=x-1+$\frac{1}{x-1}$+5≥2$\sqrt{(x-1)•\frac{1}{x-1}}$+5=2+5=7 (2分)
当且仅当x-1=$\frac{1}{x-1}$,即x=2时取等号 3分
?当x<1.
f(x)=x-1+$\frac{1}{x-1}$+5=5-[-(x-1)-$\frac{1}{x-1}$]≤-2$\sqrt{(1-x)•\frac{1}{1-x}}$+5=-2+5=3 4分
当且仅当-(x-1)=-$\frac{1}{x-1}$,即x=0时取等号
所以函数f(x)的值域(-∞,3]∪[7,+∞)…(5分)
(2)当a=0时,f(x)=$\frac{(b+1)x-3}{x-1}$<1,即$\frac{bx-2}{x-1}$<0,?(bx-2)(x-1)<0…(7分)
①当b=0时,解集为{x|x>1}…(8分)
②当b<0时,解集为{x|x>1或x<$\frac{2}{b}$}…(9分)
③当$\frac{2}{b}$=1,即b=2,解集为∅…(10分)
④当$\frac{2}{b}$>1,即0<b<2时,解集为{x|1<x<$\frac{2}{b}$};…(11分)
⑤当0<$\frac{2}{b}$<1,即b>2时,解集为{x|$\frac{2}{b}$<x<1};…(12分)
点评 本题主要考查函数值域和不等式的求解,根据分式不等式的性质转化为基本不等式以及一元二次不等式是解决本题的关键.注意要进行分类讨论.


 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案 互动课堂系列答案
互动课堂系列答案科目:高中数学 来源: 题型:填空题
| 第1 题 | 第2题 | 第3 题 | 第4 题 | 第5 题 | 第6 题 | 第7题 | 第8 题 | 得分 | |
| 甲 | × | × | √ | × | × | √ | × | √ | 5 |
| 乙 | × | √ | × | × | √ | × | √ | × | 5 |
| 丙 | √ | × | √ | √ | √ | × | × | × | 6 |
| 丁 | √ | × | × | × | √ | × | × | × | ? |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
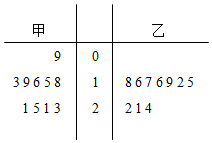 某厂为了解甲、乙两条生产线生产的产品的质量,从两条生产线生产的产品中随机抽取各10件,测量产品中某种元素的含量(单位:毫克).如图是测量数据的茎叶图:
某厂为了解甲、乙两条生产线生产的产品的质量,从两条生产线生产的产品中随机抽取各10件,测量产品中某种元素的含量(单位:毫克).如图是测量数据的茎叶图:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∨q为假 | B. | p∧q为真 | C. | (¬p)∧q为真 | D. | p∧(¬q)为真 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,$\frac{1}{2}$) | B. | (-∞,-3)∪($\frac{1}{2}$,+∞) | C. | (-2,$\frac{1}{3}$) | D. | (-∞,-2)∪($\frac{1}{3}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 64个 | B. | 72个 | C. | 84个 | D. | 96个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com