
已知数列{an}满足a1=1,a2=3,且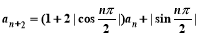 ,
,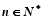 .
.
(1)证明:数列{a2k}(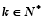 )为等比数列;
)为等比数列;
(2)求数列{an}的通项公式;
(3)设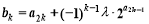 (λ为非零整数).试确定λ的值,使得对任意
(λ为非零整数).试确定λ的值,使得对任意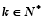 都有
都有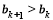 成立.
成立.
(1)见解析;(2)an= ;(3)λ=-1
;(3)λ=-1
【解析】试题分析:(1)利用等比数列的定义证明;(2)利用(1)的结论,以及a2n-1与a2n+1的关系,可以分奇偶数写出{an}的通项公式;(3)利用(1)(2)的结论,将a2k和a2k-1的表达式代入bk,再利用作差法确定λ的取值范围.过程中注意对k的奇偶情况进行讨论.
试题解析:(1)设n=2k(k∈N*)
∵a2n+2=(1+2|coskπ|)a2k+|sinkπ|=3a2k,
又a2=3,
∴当k∈N*时,数列{a2k}为首项为3,公比为3的等比数列; 3'
(2)设n=2k-1(k∈N*)
由a2k+1=(1+2|cos(k-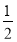 )π|)a2k-1+|sin(k-
)π|)a2k-1+|sin(k-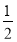 )π|=a2k-1+1
)π|=a2k-1+1
∴当k∈N*时,{a2k-1}是等差数列
∴a2k-1=a1+(k-1)·1=k 5'
又由(1)当k∈N*时,数列{a2k}为首项为3,公比为3的等比数列
∴a2k=a2·3k-1=3k 6'
综上,数列{an}的通项公式为an= 7'
7'
(3)bk=a2k+(-1)k-1λ·2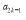 =3k+(-1)k-1λ·2k,
=3k+(-1)k-1λ·2k,
∴bk+1-bk=3k+1+(-1)kλ·2k+1-3k-(-1)k-1λ·2k
=2·3k+(-1)kλ·3·2k
由题意,对任意k∈N*都有bk+1>bk成立
∴bk+1-bk=2·3k+(-1)kλ·3·2k>0恒成立
? 2·3k>(-1)k-1λ·3·2k对任意k∈N*恒成立 9'
①当k为奇数时,2·3k>λ·3·2k ? λ<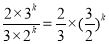 对任意k∈N*恒成立
对任意k∈N*恒成立
∵k∈N*,且k为奇数,∴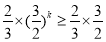 =1
=1
∴λ<1 10'
②当k为偶数时,2·3k>-λ·3·2k ? λ>- 对任意k∈N*恒成立
对任意k∈N*恒成立
∵k∈N*,且k为偶数,∴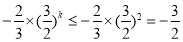 ,∴λ>-
,∴λ>-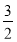 11'
11'
综上:有-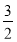 <λ<1 12'
<λ<1 12'
∵λ为非零整数,∴λ=-1.
考点:等差数列,等比数列,通项公式,不等式恒成立,分类讨论


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| 2 |
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市新都区高三诊断测试理科数学试卷(解析版) 题型:选择题
已知x,y∈(0,1),且 lnx,
lnx, ,lny成等比数列,则xy有( )
,lny成等比数列,则xy有( )
A.最小值e B.最小值 C.最大值e D.最大值
C.最大值e D.最大值
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市新都区高三诊断测试文科数学试卷(解析版) 题型:选择题
在△ABC中,三内角A,B,C成等差数列,b=6,则△ABC的外接圆半径为( )
A.6 B.12 C.2 D.4
D.4
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市高三10月考理科数学试卷(解析版) 题型:填空题
以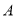 表示值域为R的函数组成的集合,
表示值域为R的函数组成的集合,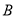 表示具有如下性质的函数
表示具有如下性质的函数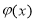 组成的集合:对于函数
组成的集合:对于函数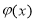 ,存在一个正数
,存在一个正数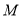 ,使得函数
,使得函数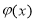 的值域包含于区间
的值域包含于区间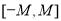 .例如,当
.例如,当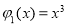 ,
,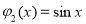 时,
时, ,
,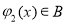 .现有如下命题:
.现有如下命题:
①设函数 的定义域为
的定义域为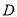 ,则“
,则“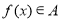 ”的充要条件是“
”的充要条件是“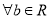 ,
,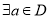 ,
,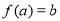 ”;
”;
②函数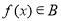 的充要条件是
的充要条件是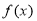 有最大值和最小值;
有最大值和最小值;
③若函数 ,
,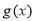 的定义域相同,且
的定义域相同,且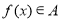 ,
,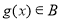 ,则
,则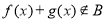 ;
;
④若函数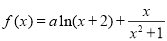 (
(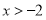 ,
,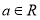 )有最大值,则
)有最大值,则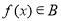 .
.
其中的真命题有 .(写出所有真命题的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com