
分析 令sinθ=t(-1≤t≤1),则y=-3b2t2-3bt+4b2+$\frac{9}{4}$,显然b≠0,对称轴为t=-$\frac{1}{2b}$,讨论对称轴和区间[-1,1]的关系,由单调性可得最大值,解方程,即可得到b的值.
解答 解:∵函数y=4b2-3b2sin2θ-3bsinθ+$\frac{9}{4}$的最大值为7,令sinθ=t(-1≤t≤1),
则y=-3b2t2-3bt+4b2+$\frac{9}{4}$,显然b≠0,对称轴为t=-$\frac{1}{2b}$.
①当-$\frac{1}{2b}$≥1,即-$\frac{1}{2}$≤b<0时,区间[-1,1]为增区间,
当t=1时,取得最大值,即有-3b2-3b+4b2+$\frac{9}{4}$=7,
解得b=$\frac{3±2\sqrt{7}}{2}$∉[-$\frac{1}{2}$,0);
②当-$\frac{1}{2b}$≤-1,即0<b≤$\frac{1}{2}$时,区间[-1,1]为减区间,
当t=-1时,取得最大值,即有-3b2+3b+4b2+$\frac{9}{4}$=7,
解得b=$\frac{-3±2\sqrt{7}}{2}$∉(0,$\frac{1}{2}$];
③当-1<-$\frac{1}{2b}$<1即为b>$\frac{1}{2}$或b<-$\frac{1}{2}$时,即有t=-$\frac{1}{2b}$时,
取得最大值7,即为$\frac{4(-{3b}^{2})•({4b}^{2}+\frac{9}{4})-{9b}^{2}}{4•(-{3b}^{2})}$=7,解得b=±1,
故答案为:±1.
点评 本题考查可化为二次函数的最值的求法,注意运用换元法和讨论对称轴和区间的关系,运用单调性解题,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | {x|0≤x<1} | B. | {x|0≤x<2} | C. | {x|0≤x≤1} | D. | {x|0≤x≤2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
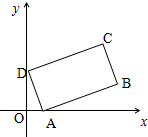 如图,矩形ABCD中AD边的长为1,AB边的长为2,矩形ABCD位于第一象限,且顶点A,D分别位于x轴、y轴的正半轴上(含原点)滑动,则$\overrightarrow{OB}•\overrightarrow{OC}$的最大值是6.
如图,矩形ABCD中AD边的长为1,AB边的长为2,矩形ABCD位于第一象限,且顶点A,D分别位于x轴、y轴的正半轴上(含原点)滑动,则$\overrightarrow{OB}•\overrightarrow{OC}$的最大值是6.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | $\sqrt{2}$ | C. | $\sqrt{10}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com