
【题目】某工厂甲、乙、丙三个车间生产了同一种产品,数量分别为120件,60件,30件.为了解它们的产品质量是否存在显著差异,用分层抽样方法抽取了一个容量为n的样本进行调查,其中从乙车间的产品中抽取了2件。
(Ⅰ)应从甲、丙两个车间的产品中分别抽取多少件,样本容量n为多少?
(Ⅱ)设抽出的n件产品分别用![]() ,
,![]() ,…,
,…,![]() 表示,现从中随机抽取2件产品。
表示,现从中随机抽取2件产品。
(i)试用所给字母列举出所有可能的抽取结果;
(ii)设M为事件“抽取的2件产品来自不同车间”,求事件M发生的概率.
【答案】(Ⅰ)答案见解析;(Ⅱ)(i)答案见解析;(ii)![]() .
.
【解析】
(Ⅰ)由题意结合分层抽样的定义确定n的值即可;
(Ⅱ)(i)由题意,利用列举法列出所有可能的结果即可;
(ii)不妨设抽出的7件产品中,来自甲车间的是![]() ,
,![]() ,
,![]() ,
,![]() ,来自乙车间的是
,来自乙车间的是![]() ,
,![]() ,来自丙车间的是
,来自丙车间的是![]() ,由题意,列出所有可能的结果,结合古典概型计算公式可得事件M发生的概率.
,由题意,列出所有可能的结果,结合古典概型计算公式可得事件M发生的概率.
(Ⅰ)解:由已知甲、乙、丙三个车间抽取产品的数量之比是4:2:1,由于采用分层抽样的方法乙车间的产品中抽取了2件产品,因此应从甲、丙两个车间分别抽取4件和1件,样本容量n为7.
(Ⅱ)(i)解:从抽出的7件产品中随机抽取两间产品的所有可能结果为
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共21种.
共21种.
(ii)解:不妨设抽出的7件产品中,来自甲车间的是![]() ,
,![]() ,
,![]() ,
,![]() ,来自乙车间的是
,来自乙车间的是![]() ,
,![]() ,来自丙车间的是
,来自丙车间的是![]() ,则从7件产品中抽取的2件产品来自不同车间的所有可能结果为
,则从7件产品中抽取的2件产品来自不同车间的所有可能结果为
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共14种.
,共14种.
所以,事件发生的概率为![]()


科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 过点
过点![]() ,且离心率为
,且离心率为![]()
(Ⅰ)求椭圆C的方程;
(Ⅱ)若过原点的直线![]() 与椭圆C交于P、Q两点,且在直线
与椭圆C交于P、Q两点,且在直线![]() 上存在点M,使得
上存在点M,使得![]() 为等边三角形,求直线
为等边三角形,求直线![]() 的方程。
的方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,若函数
时,若函数![]() 的导函数
的导函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() ,
, ![]() 两点,其横坐标分别为
两点,其横坐标分别为![]() ,
, ![]() ,线段
,线段![]() 的中点的横坐标为
的中点的横坐标为![]() ,且
,且![]() ,
, ![]() 恰为函数
恰为函数![]() 的零点,求证:
的零点,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的离心率为
的离心率为![]() ,两焦点与短轴的一个端点的连线构成的三角形面积为
,两焦点与短轴的一个端点的连线构成的三角形面积为![]() .
.
(I)求椭圆![]() 的方程;
的方程;
(II)设与圆![]() 相切的直线
相切的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点(
两点(![]() 为坐标原点),
为坐标原点),![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的正方形,
的正方形,![]() 是正三角形,
是正三角形,![]() ,
,![]() 分别是
分别是![]() 的中点。
的中点。
(1)求证:![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的大小;
所成锐二面角的大小;
(3)线段![]() 上是否存在一个动点
上是否存在一个动点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,若存在,求线段
,若存在,求线段![]() 的长度,若不存在,说明理由.
的长度,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
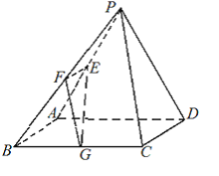
【题目】在四棱锥P﹣ABCD中,底面是边长为2的菱形,∠BAD=60°,PB=PD=2,PA![]() ,AC∩BD=O
,AC∩BD=O

(1)设平面ABP∩平面DCP=l,证明:l∥AB
(2)若E是PA的中点,求三棱锥P﹣BCE的体积VP﹣BCE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,抛物线过点
,抛物线过点![]() .
.
(Ⅰ)求抛物线![]() 的标准方程与其准线
的标准方程与其准线![]() 的方程;
的方程;
(Ⅱ)过![]() 点作直线与抛物线
点作直线与抛物线![]() 交于
交于![]() ,
,![]() 两点,过
两点,过![]() ,
,![]() 分别作抛物线的切线,证明两条切线的交点在抛物线
分别作抛物线的切线,证明两条切线的交点在抛物线![]() 的准线
的准线![]() 上.
上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com