
分析 根据题意a,b,c成等差数列,可得2b=a+c.依次对各选项进行判断.
解答 解:由题意:a,b,c成等差数列,可得2b=a+c.
对于①:∵2b=a+c,∴a+c≥2$\sqrt{ac}$,即b≥$\sqrt{ac}$,可得b2≥ac,∴①对;
对于②:$\frac{1}{a}+\frac{1}{c}=\frac{a+c}{ac}$,∵2b=a+c,∴a+c≥2$\sqrt{ac}$,可得$\frac{1}{a}+\frac{1}{c}≥\frac{2}{b}$;,∴②对;
对于③:${b^2}≤\frac{{{a^2}+{c^2}}}{2}$,∵a2+c2≥$(\frac{a+c}{2})^{2}$,2b=a+c,可得:${b^2}≤\frac{{{a^2}+{c^2}}}{2}$,∴③对;
对于④:a,b,c成等差数列,可得2b=a+c,可得2sinB=sinA+sinC,∵A+B+C=π,
可得:B≤$\frac{π}{3}$.∴④对.
故答案为:①②③④.
点评 本题考查了基本不等式的性质、等差数列的基本性质.考查了计算能力,属于基础题.


科目:高中数学 来源: 题型:选择题
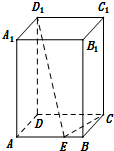 如图,在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=$\sqrt{3}$,点E为棱AB上的动点,则D1E+CE的最小值为( )
如图,在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=$\sqrt{3}$,点E为棱AB上的动点,则D1E+CE的最小值为( )| A. | $2\sqrt{2}$ | B. | $\sqrt{10}$ | C. | $2+\sqrt{2}$ | D. | $\sqrt{5}+1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${a_n}={({-1})^{n+1}}({2n+1})$ | B. | ${a_n}={({-1})^{n+1}}({2n-1})$ | C. | ${a_n}={({-1})^n}({2n+1})$ | D. | ${a_n}={({-1})^n}({2n-1})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{10}$ | B. | $\frac{9}{20}$ | C. | $\frac{20}{21}$ | D. | $\frac{10}{21}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com