
分析 利用函数的奇偶性求函数g(x)的解析式,再利用g(x)得单调性解对数不等式,求得x的范围.
解答 解:函数y=f(x)是定义在[-4,4]上的偶函数,
且f(x)=$\left\{\begin{array}{l}{{3}^{x}-9,0≤x≤4}\\{g(x),-4≤x<0}\end{array}\right.$,则g(x)=3-x-9,故g(x)的零点为-2.
由不等式(1-2x)g(log2x)<0,可得$\left\{\begin{array}{l}{1-2x<0}\\{g(_{log2}x)>0}\end{array}\right.$ ①,或$\left\{\begin{array}{l}{1-2x>0}\\{g{(log}_{2}x)<0}\end{array}\right.$②.
由①可得$\left\{\begin{array}{l}{x>\frac{1}{2}}\\{{-4≤log}_{2}x<-2}\end{array}\right.$,∴x∈∅.
由②可得$\left\{\begin{array}{l}{x<\frac{1}{2}}\\{{-2<log}_{2}x≤0}\end{array}\right.$,∴$\frac{1}{4}$<x<$\frac{1}{2}$,
故答案为:($\frac{1}{4}$,$\frac{1}{2}$).
点评 本题主要考查利用函数的奇偶性求函数的解析式,解对数不等式,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
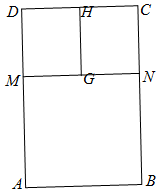 拟用长度为l的钢筋焊接一个如图所示的矩形框架结构(钢筋体积、焊接点均忽略不计),其中G、H分别为框架梁MN、CD的中点,MN∥CD,设框架总面积为S平方米,BN=2CN=2x米.
拟用长度为l的钢筋焊接一个如图所示的矩形框架结构(钢筋体积、焊接点均忽略不计),其中G、H分别为框架梁MN、CD的中点,MN∥CD,设框架总面积为S平方米,BN=2CN=2x米.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2016}{2017}$ | B. | $\frac{2017}{2016}$ | C. | $\frac{2015}{2017}$ | D. | $\frac{2015}{2016}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com