Question

若a,b,c均为正数，且a+b+c=6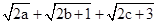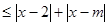，对任意x∈R恒成立，求m的取值范围.

Answer 1

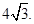m≤2-或m≥2+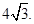

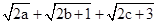
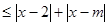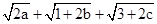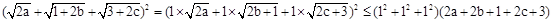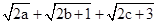解析试题分析：由题意可得要使对任意x∈R恒成立.及要求出的最大值.由柯西不等式可得=48.有最大值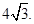所以得到|x-2|+|x-m|≥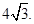对任意的x∈R恒成立.即对任意的x恒成立所以应该使|x-2|+|x-m|的最小值大于或等于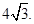再通过绝对值不等式即可得m的取值范围.本题综合性较强，应用了两个重要不等式.同时应用两次不等式恒成立的问题.
试题解析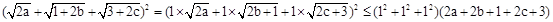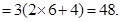：所以
∴
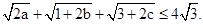
当且仅当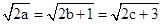即2a=2b+1=2c+3时等号成立，       4分
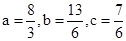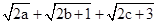又a+b+c=6，∴时，有最大值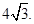
∴|x-2|+|x-m|≥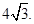对任意的x∈R恒成立.
∵|x-2|+|x-m|≥|(x-2)-(x-m)| =|m-2|,
∴|m-2|≥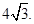
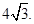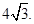解得m≤2-或m≥2+       7分
考点：1.柯西不等式.2.绝对值不等式.3.不等式的恒成立问题.