Question

已知a,b,c为互不相等的非负数，求证：a²+b²+c²＞(++).

Answer 1

见解析

解析试题分析：因为a,b,c为互不相等的非负数，由重要不等式得，a²+b²＞2ab，b²+c²＞2bc，a²+c²＞2ac，利用同向不等式的加法原则得，a²+b²+c²＞ab+bc+ac，由基本不等式得ab+bc＞2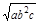 ，bc+ac＞2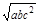，ab+ac＞2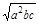，再利用加法原则得，ab+bc+ac＞(++)，再利用不等式的传递性即得所要证明的结论.
试题解析：证明 ∵a²+b²≥2ab,b²+c²≥2bc,a²+c²≥2ac.
又∵a,b,c为互不相等的非负数，
∴上面三个式子中都不能取“=”，
∴a²+b²+c²＞ab+bc+ac,
∵ab+bc≥2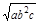,bc+ac≥2,
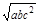ab+ac≥2,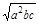
又a,b,c为互不相等的非负数，
∴ab+bc+ac＞(++),
∴a²+b²+c²＞(++)       （14分）
考点：重要不等式；基本不等式；不等式性质