
【题目】随着移动互联网的快速发展,基于互联网的共享单车应运而生.某市场研究人员为了了解共享单车运营公司M的经营状况,对该公司最近六个月内的市场占有率进行了统计,并绘制了相应的折线图.
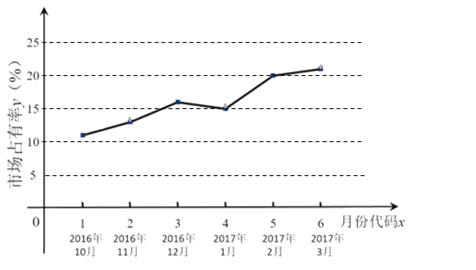
(Ⅰ)由折线图可以看出,可用线性回归模型拟合月度市场占有率y与月份代码x之间的关系.求y关于x的线性回归方程,并预测M公司2017年4月份(即x=7时)的市场占有率;
(Ⅱ)为进一步扩大市场,公司拟再采购一批单车.现有采购成本分别为1000元/辆和1200元/辆的A、B两款车型可供选择,按规定每辆单车最多使用4年,但由于多种原因(如骑行频率等)会导致车辆报废年限各不相同.考虑到公司运营的经济效益,该公司决定先对两款车型的单车各100辆进行科学模拟测试,得到两款单车使用寿命频数表如下:
车型 | 1年 | 2年 | 3年 | 4年 | 总计 |
A | 20 | 35 | 35 | 10 | 100 |
B | 10 | 30 | 40 | 20 | 100 |
经测算,平均每辆单车每年可以带来收入500元.不考虑除采购成本之外的其他成本,假设每辆单车的使用寿命都是整数年,且以频率作为每辆单车使用寿命的概率.如果你是M公司的负责人,以每辆单车产生利润的期望值为决策依据,你会选择采购哪款车型?
参考数据: ![]()
![]()
(参考公式:回归直线方程为![]() ,其中
,其中 )
)
【答案】(1)23%(2)A
【解析】试题分析:利用![]() 计算
计算![]() 和
和![]() ,再计算
,再计算![]() ,根据回归直线过样本中心点
,根据回归直线过样本中心点![]() ,求出
,求出![]() 得出回归直线方程;令
得出回归直线方程;令![]() ,求出预测的月度市场占有率,再根据概率值求出两款车型产生的利润的数学期望,比较后,决策采购哪款.
,求出预测的月度市场占有率,再根据概率值求出两款车型产生的利润的数学期望,比较后,决策采购哪款.
试题解析:(1)由折线图中所给的数据计算可得![]() ,
,
![]() 。…2分 ∴
。…2分 ∴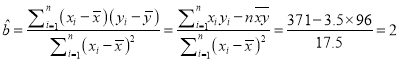 …5分
…5分
∴![]() .
.
∴月度市场占有率![]() 与月份序号
与月份序号![]() 之间的线性回归方程为
之间的线性回归方程为![]() .
.
当![]() 时,
时, ![]() .
.
故![]() 公司2017年4月份的市场占有率预计为23%.
公司2017年4月份的市场占有率预计为23%.
(2)由频率估计概率,每辆![]() 款车可使用1年、2年、3年和4年的概率分别为0.2、0.35、0.35和0.1,
款车可使用1年、2年、3年和4年的概率分别为0.2、0.35、0.35和0.1,
∴每辆![]() 款车可产生的利润期望值为
款车可产生的利润期望值为
![]() (元).
(元).
由频率估计概率,每辆![]() 款车可使用1年、2年、3年和4年的概率分别为0.1、0.3、0.4和0.2,
款车可使用1年、2年、3年和4年的概率分别为0.1、0.3、0.4和0.2,
∴每辆![]() 款车可产生的利润期望值为:
款车可产生的利润期望值为:
![]() (元),
(元),
∵![]() ,∴应该采购
,∴应该采购![]() 款单车.
款单车.


科目:高中数学 来源: 题型:
【题目】自驾游从![]() 地到
地到![]() 地有甲乙两条线路,甲线路是
地有甲乙两条线路,甲线路是![]() ,乙线是
,乙线是![]() ,其中
,其中![]() 段、
段、![]() 段、
段、![]() 段都是易堵车路段.假设这三条路段堵车与否相互独立.这三条路段的堵车概率及平均堵车时间如表1所示.经调查发现,堵车概率
段都是易堵车路段.假设这三条路段堵车与否相互独立.这三条路段的堵车概率及平均堵车时间如表1所示.经调查发现,堵车概率![]() 在
在![]() 上变化,
上变化, ![]() 在
在![]() 上变化.在不堵车的情况下.走线路甲需汽油费500元,走线路乙需汽油费545元.而每堵车1小时,需多花汽油费20元.路政局为了估计
上变化.在不堵车的情况下.走线路甲需汽油费500元,走线路乙需汽油费545元.而每堵车1小时,需多花汽油费20元.路政局为了估计![]() 段平均堵车时间,调查了100名走甲线路的司机,得到表2数据.
段平均堵车时间,调查了100名走甲线路的司机,得到表2数据.
CD段 | EF段 | GH段 | |||
堵车概率 |
|
|
| ||
平均堵车时间 (单位:小时) |
| 2 | 1 | ||
(表1) | |||||
堵车时间(单位:小时) | 频数 | ||||
| 8 | ||||
| 6 | ||||
| 38 | ||||
| 24 | ||||
| 24 | ||||
(表2) | |||||
(1)求![]() 段平均堵车时间
段平均堵车时间![]() 的值.
的值.
(2)若只考虑所花汽油费期望值的大小,为了节约,求选择走甲线路的概率.
(3)在(2)的条件下,某4名司机中走甲线路的人数记为X,求X的数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
, ![]() (
(![]() ).
).
(Ⅰ)求函数![]() 的单调增区间;
的单调增区间;
(Ⅱ)当![]() 时,记
时,记![]() ,是否存在整数
,是否存在整数![]() ,使得关于
,使得关于![]() 的不等式
的不等式![]() 有解?若存在,请求出
有解?若存在,请求出![]() 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从一批土鸡蛋中,随机抽取n个得到一个样本,其重量(单位:克)的频数分布表如表:
分组(重量) | [80,85) | [85,90) | [90,95) | [95,100] |
频数(个) | 10 | 50 | m | 15 |
已知从n个土鸡蛋中随机抽取一个,抽到重量在在[90,95)的土鸡蛋的根底为 ![]()
(1)求出n,m的值及该样本的众数;
(2)用分层抽样的方法从重量在[80,85)和[95,100)的土鸡蛋中共抽取5个,再从这5个土鸡蛋中任取2 个,其重量分别是g1 , g2 , 求|g1﹣g2|≥10概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ﹣
﹣ ![]() .
.
(1)判断f(x)的奇偶性;
(2)判断f(x)的单调性,并用定义证明;
(3)解不等式f(f(x))+f( ![]() )<0.
)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平行六面体ABCD﹣A1B1C1D1中,侧棱B1B长为3,底面是边长为2的菱形,∠A1AB=120°,∠A1AD=60°,点E在棱B1B上,则AE+C1E的最小值为( )
A.![]()
B.5
C.2![]()
D.7
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)若函数![]() 在
在![]() 处的切线平行于直线
处的切线平行于直线![]() ,求实数a的值;
,求实数a的值;
(Ⅱ)判断函数![]() 在区间
在区间![]() 上零点的个数;
上零点的个数;
(Ⅲ)在(Ⅰ)的条件下,若在![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)对定义域R内的任意x都有f(x)=f(4﹣x),且当x≠2时其导函数f′(x)满足(x﹣2)f′(x)>0,若2<a<4则( )
A.f(2a)<f(3)<f(log2a)
B.f(log2a)<f(3)<f(2a)
C.f(3)<f(log2a)<f(2a)
D.f(log2a)<f(2a)<f(3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com