
分析 由等比数列的前n项和公式得a1=1,由此利用等比数列的性质能求出S2+S4+S6+S8+S10.
解答 解:∵等比数列{an}的前n项和为Sn,公比q=2,S10=1023,
∴${S}_{10}=\frac{{a}_{1}(1-{2}^{10})}{1-2}$=1023,
解得a1=1,
∴S2+S4+S6+S8+S10
=$\frac{1×(1-{2}^{2})}{1-2}$+$\frac{1×(1-{2}^{4})}{1-2}$+$\frac{1×(1-{2}^{6})}{1-2}$+$\frac{1×(1-{2}^{8})}{1-2}$+$\frac{1×(1-{2}^{10})}{1-2}$
=22+24+26+28+210-5
=$\frac{4(1-{4}^{5})}{1-4}$-5
=1359.
故答案为:1359.
点评 本题考查等比数列中若干项和的求法,是基础题,解题时要认真审题,注意等比数列的性质的合理运用.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
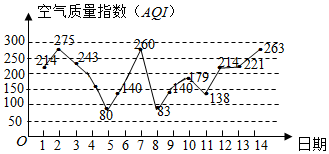 如图所示是某市2016年2月1日至14日的空气质量指数趋势图,空气质量指数(AQI)小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某同志随机选择2月1日至2月12日中的某一天到达该市,并停留3天.该同志到达当日空气质量优良的概率$\frac{1}{6}$.
如图所示是某市2016年2月1日至14日的空气质量指数趋势图,空气质量指数(AQI)小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某同志随机选择2月1日至2月12日中的某一天到达该市,并停留3天.该同志到达当日空气质量优良的概率$\frac{1}{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜欢看该节目 | 不喜欢看该节目 | 合计 | |
| 女生 | 5 | ||
| 男生 | 10 | ||
| 合计 | 50 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.0050. | 001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在区间[-$\frac{π}{12}$,$\frac{5}{12}$π]上单调递增 | B. | 在区间[$\frac{π}{4},\frac{π}{4}$]上单调递增 | ||
| C. | 在区间[$\frac{π}{4}$,$\frac{3π}{4}$]上单调递减 | D. | 在区间[-$\frac{π}{12}$,$\frac{5}{12}$π]上单调递减 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com