
分析 (1)根据向量的数量积公式计算即可,
(2)根据向量的模的计算方法计算即可,
(3)根据向量垂直得到数量积为0,即可到关于k的方程,解得即可.
解答 解:(1)∵向量$\overrightarrow a$与$\overrightarrow b$的夹角为120°,且|$\overrightarrow a$|=4,|$\overrightarrow b$|=2,
∴$\overrightarrow a$•$\overrightarrow b$=|$\overrightarrow a$|•|$\overrightarrow b$|•cos120°=4×2×(-$\frac{1}{2}$)=-4,
(2)|3$\overrightarrow a$+5$\overrightarrow b$|2=9|$\overrightarrow a$|2+25|$\overrightarrow b$|2+30•$\overrightarrow a$•$\overrightarrow b$=9×16+25×4-30×4=124,
∴|3$\overrightarrow a$+5$\overrightarrow b$|=2$\sqrt{31}$,
(3)∵向量$\overrightarrow a$+k$\overrightarrow b$与5$\overrightarrow a$+2$\overrightarrow b$垂直,
∴($\overrightarrow a$+k$\overrightarrow b$)•(5$\overrightarrow a$+2$\overrightarrow b$)=0,
∴5|$\overrightarrow a$|2+2k|$\overrightarrow b$|2+(5k+2)•$\overrightarrow a$•$\overrightarrow b$=0,
∴5×16+8k-4(5k+2)=0,
解得k=6.
点评 本题考查了向量的数量积的运算,模的计算和向量的垂直的条件,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
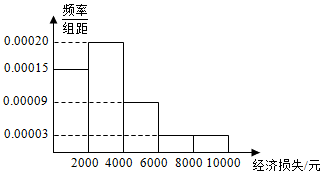 2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,造成直接经济损失12.99亿元.适逢暑假,小明调查了某小区的50户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出如图频率分布直方图.
2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,造成直接经济损失12.99亿元.适逢暑假,小明调查了某小区的50户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出如图频率分布直方图.| 经济损失不超过 4000元 | 经济损失超过 4000元 | 合计 | |
| 捐款超过 500元 | 30 | ||
| 捐款不超 过500元 | 6 | ||
| 合计 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | Sn的最小值为100 | B. | Sn的最大值为400 | C. | Sn<500 | D. | Sn≤500 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com