
| A. | 2013 | B. | 2014 | C. | 2015 | D. | 2016 |
分析 先求出a1,a2,a3,能等比数列的性质求出t=-1,由此能求出a1的值.
解答 解:∵等比数列{an}的前n项和Sn=2016n+t(t为常数),
∴${a}_{1}={S}_{1}{{=2016}_{\;}}^{1}$+t=2016+t,
a2=S2-S1=20162+t-(2016+t)=4062240,
a3=S3-S2=20163+t-(20162+t)=8189475840,
∵${{a}_{2}}^{2}={a}_{1}{a}_{3}$,
∴40622402=(2016+t)×8189475840,
解得t=-1,
∴a1=2016+(-1)=2015.
故选:C.
点评 本题考查等比数列中首项的求法,是基础题,解题时要认真审题,注意a1的值的求法.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{(5π-6\sqrt{3})^{2}}{18}$ | B. | $\frac{(5π+6\sqrt{3})^{2}}{18}$ | C. | $\frac{{π}^{2}}{18}$ | D. | $\frac{{π}^{2}}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 当x>0且x≠1时,lgx+$\frac{1}{lgx}$≥2 | |
| B. | 当x>0时,$\sqrt{x}$+$\frac{1}{\sqrt{x}}$≥2 | |
| C. | 当0<θ≤$\frac{π}{2}$时,sinθ+$\frac{2}{sinθ}$的最小值为2$\sqrt{2}$ | |
| D. | 当-$\frac{1}{2}$≤x<0时,x+$\frac{1}{x}$有最大值-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2π | B. | 2$\sqrt{6}$π | C. | 6π | D. | 12π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
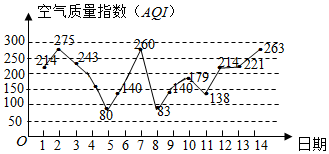 如图所示是某市2016年2月1日至14日的空气质量指数趋势图,空气质量指数(AQI)小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某同志随机选择2月1日至2月12日中的某一天到达该市,并停留3天.该同志到达当日空气质量优良的概率$\frac{1}{6}$.
如图所示是某市2016年2月1日至14日的空气质量指数趋势图,空气质量指数(AQI)小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某同志随机选择2月1日至2月12日中的某一天到达该市,并停留3天.该同志到达当日空气质量优良的概率$\frac{1}{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com