
【题目】如图,已知四棱锥中,四边形![]() 为矩形,
为矩形,![]() ,
,![]() ,
,![]() .
.
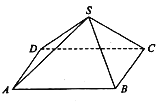
(1)求证:![]() 平面
平面![]() ;
;
(2)设![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成的二面角的正弦值.
所成的二面角的正弦值.
【答案】(1)见证明;(2)![]()
【解析】
(1)证明BC![]() 平面SDC,即可证得AD
平面SDC,即可证得AD![]() 平面SDC,即可证得SC
平面SDC,即可证得SC![]() AD,利用SC2+SD2=DC2证得SC
AD,利用SC2+SD2=DC2证得SC![]() SD,问题得证。
SD,问题得证。
(2)以点O为原点,建立坐标系如图,求得S(0,0,![]() ),C(0,
),C(0,![]() ,0), A(2,-
,0), A(2,-![]() ,0),B(2,
,0),B(2,![]() ,0),利用
,0),利用![]() 即可求得E(2,
即可求得E(2,![]() ,0),求得
,0),求得![]()
![]() ,
,![]()
![]() ,利用空间向量夹角公式计算即可得解。
,利用空间向量夹角公式计算即可得解。
(1)证明: BC![]() SD ,BC
SD ,BC![]() CD
CD
则BC![]() 平面SDC, 又
平面SDC, 又![]()
则AD![]() 平面SDC,
平面SDC,![]() 平面SDC
平面SDC
SC![]() AD
AD
又在△SDC中,SC=SD=2, DC=AB![]() ,故SC2+SD2=DC2
,故SC2+SD2=DC2
则SC![]() SD ,又
SD ,又![]()
所以 SC![]() 平面SAD
平面SAD
(2)解:作SO![]() CD于O,因为BC
CD于O,因为BC![]() 平面SDC,
平面SDC,
所以平面ABCD![]() 平面SDC,故SO
平面SDC,故SO![]() 平面ABCD
平面ABCD
以点O为原点,建立坐标系如图.
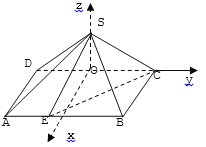
则S(0,0,![]() ),C(0,
),C(0,![]() ,0), A(2,-
,0), A(2,-![]() ,0),B(2,
,0),B(2,![]() ,0)
,0)
设E(2,y,0),因为![]()
所以![]() 即E((2,
即E((2,![]() ,0)
,0)
![]()
![]()
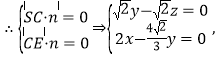 令
令![]() ,则
,则![]() ,
,![]()
![]()
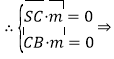
![]() ,令
,令![]() ,则
,则![]() ,
,![]()
![]()
![]()
所以所求二面角的正弦值为![]()


科目:高中数学 来源: 题型:
【题目】对以下命题:
①随机事件的概率与频率一样,与试验重复的次数有关;
②抛掷两枚均匀硬币一次,出现一正一反的概率是![]() ;
;
③若一种彩票买一张中奖的概率是![]() ,则买这种彩票一千张就会中奖;
,则买这种彩票一千张就会中奖;
④“姚明投篮一次,求投中的概率”属于古典概型概率问题.
其中正确的个数是( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如城镇小汽车的普及率为75%,即平均每100个家庭有75个家庭拥有小汽车,若从如城镇中任意选出5个家庭,则下列结论成立的是( )
A.这5个家庭均有小汽车的概率为![]()
B.这5个家庭中,恰有三个家庭拥有小汽车的概率为![]()
C.这5个家庭平均有3.75个家庭拥有小汽车
D.这5个家庭中,四个家庭以上(含四个家庭)拥有小汽车的概率为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解居民消费情况,某地区调查了10000户小家庭的日常生活平均月消费金额,根据所得数据绘制了样本频率分布直方图,如图所示,每户小家庭的平均月消费金额均不超过9千元,其中第六组第七组第八组尚未绘制完成,但是已知这三组的频率依次成等差数列,且第六组户数比第七组多500户,
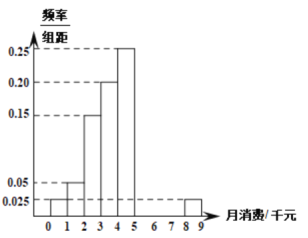
(1)求第六组第七组第八组的户数,并补画图中所缺三组的直方图;
(2)若定义月消费在3千元以下的小家庭为4类家庭,定义月消费在3千元至6千无的小家庭为B类家庭,定义月消费6千元以上的小家庭为C类家庭,现从这10000户家庭中按分层抽样的方法抽取80户家庭召开座谈会,间A,B,C各层抽取的户数分别是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校组织的一次教师招聘共分笔试和面试两个环节,笔试环节共有20名大学毕业生参加,其中男、女生的比例恰好为![]() ,其成绩的茎叶图如图所示.假设成绩在90分以上的考生可以进入面试环节.
,其成绩的茎叶图如图所示.假设成绩在90分以上的考生可以进入面试环节.
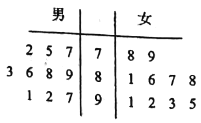
(1)试比较男、女两组成绩平均分的大小,并求出女生组的方差;
(2)从男、女两组可以进入面试环节的考生中分别任取1人,求两人分差不小于3分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,用四种不同颜色给图中的A,B,C,D,E,F六个点涂色,要求每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色,则不同的涂色方法用
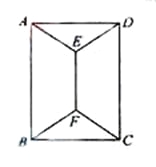
A.288种B.264种C.240种D.168种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两人各自独立的参加某单位面试,规定每位考生需要从编号为1-6的6道面试题中随机抽出3道进行面试,至少答对两道才能合格.已知甲能答对其中3道题,乙能答对其中4道题.
(1)求甲恰好答对两道题的概率.
(2)求甲合格且乙不合格的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com