
分析 先化简函数的解析式,在同一个坐标系下画出函数$y=\frac{{|{{x^2}-1}|}}{x-1}$的图象与函数y=2x+b图象,结合图象,可得实数b的取值范围.
解答 解:当x>1或x<-1时,y=x+1,
当-1≤x<1时,y=-x+1,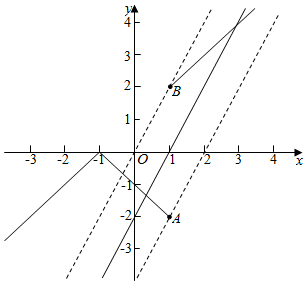
当直线y=2x+b经过点A(1,-2)时,此时-2=2+b,解得b=-4时只有一个交点,
当直线y=2x+b经过点B(,2)时,此时2=2+b,解得b=0,此时只有一个交点,
由图象可知,函数$y=\frac{{|{{x^2}-1}|}}{x-1}$的图象与函数y=2x+b的图象恰有两个交点,则实数b的取值范围是(-4,0)
故答案为:(-4,0).
点评 本题主要考查了根的存在性及根的个数判断,同时考查了作图能力和分类讨论的数学思想,属于基础题.


 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x+y-2=0 | B. | x-y+3=0 | C. | x+y-3=0 | D. | x-y+2=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{32}$ | B. | $\frac{1}{16}$ | C. | $\frac{1}{64}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
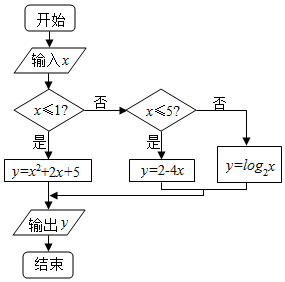
| A. | 2 | B. | ${log_2}\frac{π}{2}$ | C. | 2-2π | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
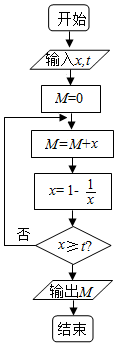
| A. | 3 | B. | $\frac{11}{3}$ | C. | $\frac{19}{6}$ | D. | $\frac{37}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com