
分析 (1)直接对f(x)求导,化简即可.又因为x>1,可得f'(x)>0;
(2)利用换元t=$\frac{{x}_{2}}{{x}_{1}}$,构造g(t)=lnt-$\frac{2(t-1)}{{t}^{2}+1}$>g(1)=0,从而化简得证;
(3)由(1)得t>1时,lnt>$\frac{2(t-1)}{{t}^{2}+1}$,得出:$ln\frac{n+1}{n}$>$\frac{n}{(n+1)^{2}}$,从而利用累加法可得证;
解答 证明:(1)当a=1时,f(x)=lnx-$\frac{2(x-1)}{{x}^{2}+1}$ (x>0);
f'(x)=$\frac{1}{x}$-$\frac{2({x}^{2}+1)-2(x-1)•2x}{({x}^{2}+1)^{2}}$;
=$\frac{{x}^{4}+2{x}^{3}-2{x}^{2}-2x+1}{x({x}^{2}+1)^{2}}$;
=$\frac{(x-1)({x}^{3}+3{x}^{2}+x-1)}{x({x}^{2}+1)^{2}}$≥0;
故当x≥1时,f'(x)≥0;
所以,x∈[1,+∞)时,f(x)恒为增函数;
解:(2)令t=$\frac{{x}_{2}}{{x}_{1}}$>1,由(1)得g(t)=lnt-$\frac{2(t-1)}{{t}^{2}+1}$>g(1)=0;
∴lnt>$\frac{2(t+1)}{{t}^{2}+1}$ 即$ln\frac{{x}_{2}}{{x}_{1}}$>$\frac{2(\frac{{x}_{2}}{{x}_{1}}-1)}{(\frac{{x}_{2}}{{x}_{1}})^{2}+1}$;
∴lnx2-lnx1>$\frac{2{x}_{1}({x}_{2}-{x}_{1})}{{x}_{1}^{2}+{x}_{2}^{2}}$;
(3)由(1)得t>1时,lnt>$\frac{2(t-1)}{{t}^{2}+1}$;
∴$ln\frac{n+1}{n}$>$\frac{2(\frac{n+1}{n}-1)}{(\frac{n+1}{n})^{2}+1}$=$\frac{2n}{(n+1)^{2}+{n}^{2}}$>$\frac{2n}{(n+1)^{2}+(n+1)^{2}}$=$\frac{n}{(n+1)^{2}}$;
∴$ln\frac{2}{1}>\frac{1}{{2}^{2}}$;
$ln\frac{3}{2}>\frac{2}{{3}^{2}}$;
…
$ln\frac{n+1}{n}$>$\frac{n}{(n+1)^{2}}$;
利用累加法后:$ln\frac{2}{1}$+$ln\frac{3}{2}$+…+$ln\frac{n+1}{n}$>$\frac{1}{{2}^{2}}+\frac{2}{{3}^{2}}+…+\frac{n}{(n+1)^{2}}$;
得证:ln(n+1)>$\frac{1}{{2}^{2}}+\frac{2}{{3}^{2}}+\frac{3}{{4}^{2}}+…+\frac{n}{(n+1)^{2}}$.
点评 本题主要考查了利用导数研究函数的单调性,构造法与累加法以及不等式缩放等知识点综合应用,属中等题.


科目:高中数学 来源: 题型:选择题

| A. | 计算小于100的奇数的连乘积 | |
| B. | 计算从1开始的连续奇数的连乘积 | |
| C. | 从1开始的连续奇数的连乘积,当乘积大于100时,计算奇数的个数 | |
| D. | 计算1×3×5×…×n≥100时的最小的n值. |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
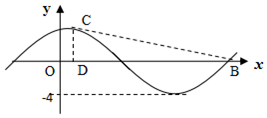 已知函数f(x)=Asin($\frac{1}{2}$x+φ),x∈R,(其中,|φ|<$\frac{π}{2}$)的部分图象如图所示,设点($\frac{2π}{3}$,4)是图象上y轴右侧的第一个最高点,CD⊥DB,D是y轴右侧第二个对称中心,则△DBC的面积是( )
已知函数f(x)=Asin($\frac{1}{2}$x+φ),x∈R,(其中,|φ|<$\frac{π}{2}$)的部分图象如图所示,设点($\frac{2π}{3}$,4)是图象上y轴右侧的第一个最高点,CD⊥DB,D是y轴右侧第二个对称中心,则△DBC的面积是( )| A. | 3 | B. | 4π | C. | 6π | D. | 12π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
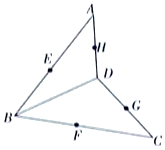 如图,在空间四边形ABCD(A,B,C,D不共面)中,一个平面与边AB,BC,CD,DA分别交于E,F,G,H(不含端点),则下列结论错误的是( )
如图,在空间四边形ABCD(A,B,C,D不共面)中,一个平面与边AB,BC,CD,DA分别交于E,F,G,H(不含端点),则下列结论错误的是( )| A. | 若AE:BE=CF:BF,则AC∥平面EFGH | |
| B. | 若E,F,G,H分别为各边中点,则四边形EFGH为平行四边形 | |
| C. | 若E,F,G,H分别为各边中点且AC=BD,则四边形EFGH为矩形 | |
| D. | 若E,F,G,H分别为各边中点且AC⊥BD,则四边形EFGH为矩形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com