
分析 由AC边上的高BH所在直线方程为x-2y-5=0可得直线BH的斜率为$\frac{1}{2}$,根据垂直时斜率乘积为-1可得直线AC的斜率为-2,且过(1,2)即可得到AC边所在直线方程,与x-2y-5=0联立,可得C,即可求AC边的长.
解答 解:由AC边上的高BH所在直线方程为x-2y-5=0可知kAC=-2,
又A(1,2),AC边所在直线方程为y-2=-2(x-1),
即AC边所在直线方程为2x+y-4=0.
与x-2y-5=0联立,可得C($\frac{13}{5}$,-$\frac{6}{5}$),
∴|AC|=$\sqrt{(1-\frac{13}{5})^{2}+(2+\frac{6}{5})^{2}}$=$\frac{8\sqrt{5}}{5}$.
点评 考查学生掌握两直线垂直时满足斜率乘积为-1的条件,会求两直线的交点坐标,以及会根据斜率和一点坐标写出直线的一般式方程.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=|x|,$g(x)=\sqrt{x^2}$ | B. | f(x)=2x,g(x)=2(x+1) | ||
| C. | $f(x)=\sqrt{{{(-x)}^2}}$,$g(x)={(\sqrt{-x})^2}$ | D. | $f(x)=\frac{{{x^2}+x}}{x+1}$,g(x)=x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
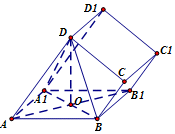 四棱柱ABCD-A1B1C1D1中,底面ABCD是梯形,AD∥BC,侧面ABB1A1是菱形,∠DAB=∠DAA1.
四棱柱ABCD-A1B1C1D1中,底面ABCD是梯形,AD∥BC,侧面ABB1A1是菱形,∠DAB=∠DAA1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{2}{3}$,+∞) | B. | (1,+∞) | C. | ($\frac{1}{3}$,+∞) | D. | (-$\frac{1}{3}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | e-$\frac{1}{e}$ | B. | e-1 | C. | e2-1 | D. | $\frac{1}{e}$-e |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com