
°ĺŐ‚ńŅ°Ņ“—÷™ń≥÷÷…Ő∆∑√Ņ»’ĶńŌķ ŘŃŅy£®Ķ•őĽ£ļ∂÷£©”ŽŌķ ؾسŮx£®Ķ•őĽ£ļÕÚ‘™/∂÷£¨1£ľx°‹5£©¬ķ◊„£ļĶĪ1£ľx°‹3 Ī£¨y=a£®x©Ā4£©2 +![]() £®aő™≥£ ż£©£ĽĶĪ3£ľx°‹5 Ī£¨y=kx+7£®k£ľ0£©£¨“—÷™ĶĪŌķ ؾسŮő™3ÕÚ‘™/∂÷ Ī£¨√Ņ»’Ņ… Ř≥Ųł√…Ő∆∑4∂÷£¨«“Ōķ ؾسŮx° £®3£¨5]ĪšĽĮ Ī£¨Ōķ ŘŃŅ◊ÓĶÕő™2∂÷£ģ
£®aő™≥£ ż£©£ĽĶĪ3£ľx°‹5 Ī£¨y=kx+7£®k£ľ0£©£¨“—÷™ĶĪŌķ ؾسŮő™3ÕÚ‘™/∂÷ Ī£¨√Ņ»’Ņ… Ř≥Ųł√…Ő∆∑4∂÷£¨«“Ōķ ؾسŮx° £®3£¨5]ĪšĽĮ Ī£¨Ōķ ŘŃŅ◊ÓĶÕő™2∂÷£ģ
£®1£©«ůa£¨kĶń÷Ķ£¨≤Ę»∑∂®yĻō”ŕxĶńļĮ żĹ‚őŲ Ĺ£Ľ
£®2£©»Űł√…Ő∆∑ĶńŌķ Ř≥…Īĺő™1ÕÚ‘™/∂÷£¨ ‘»∑∂®Ōķ ؾسŮxĶń÷Ķ£¨ ĻĶ√√Ņ»’Ōķ Řł√…Ő∆∑ňýĽŮņŻ»ů◊Óīů£ģ
°ĺīūįł°Ņ£®1£©![]() £¨
£¨ £Ľ
£Ľ
£®2£©x=2ÕÚ‘™/∂÷ Ī£¨√Ņ»’Ōķ Řł√…Ő∆∑ňýĽŮņŻ»ů◊Óīů£ģ
°ĺĹ‚őŲ°Ņ
‘Ő‚∑÷őŲ£ļ£®1£©łý囓—÷™łÝ≥ŲĶńĪŪīÔ Ĺ£¨”…ŐűľĢ°įŌķ ؾسŮő™3ÕÚ‘™/∂÷ Ī£¨√Ņ»’Ņ… Ř≥Ųł√…Ő∆∑4∂÷£¨«“Ōķ ؾسŮx° £®3£¨5]ĪšĽĮ Ī£¨Ōķ ŘŃŅ◊ÓĶÕő™2∂÷°Ī£¨Ņ…«ůĶ√![]() £¨ī”∂ÝļĮ żĹ‚őŲ Ĺ£¨◊Ę“‚Ĺ‚őŲ Ĺ «∑÷∂őļĮ ż£Ľ
£¨ī”∂ÝļĮ żĹ‚őŲ Ĺ£¨◊Ę“‚Ĺ‚őŲ Ĺ «∑÷∂őļĮ ż£Ľ
£®2£©”…£®1£©÷–ňýĶ√Ōķ ŘŃŅ≥ň“‘![]() Ņ…Ķ√ņŻ»ů£¨ĶĪ1£ľx°‹3 Ī£¨ņŻ»ůő™
Ņ…Ķ√ņŻ»ů£¨ĶĪ1£ľx°‹3 Ī£¨ņŻ»ůő™![]()
![]() £¨ņŻ”√Ķľ żĶń÷™ ∂Ņ…«ůĶ√īň ĪĶń◊Óīů÷Ķ£¨ĶĪ3£ľx°‹5 Ī£¨√Ņ»’Ōķ ŘņŻ»ůf£®x£©=£®©Āx+7£©£®x©Ā1£©=©Āx2+8x©Ā7£¨”…∂ĢīőļĮ żĶń–‘÷ Ņ…«ůĶ√īň ĪĶń◊Óīů÷Ķ£¨ŃĹ’ŖĪ»ĹŌŅ…Ķ√◊Óīů÷Ķ£ģ
£¨ņŻ”√Ķľ żĶń÷™ ∂Ņ…«ůĶ√īň ĪĶń◊Óīů÷Ķ£¨ĶĪ3£ľx°‹5 Ī£¨√Ņ»’Ōķ ŘņŻ»ůf£®x£©=£®©Āx+7£©£®x©Ā1£©=©Āx2+8x©Ā7£¨”…∂ĢīőļĮ żĶń–‘÷ Ņ…«ůĶ√īň ĪĶń◊Óīů÷Ķ£¨ŃĹ’ŖĪ»ĹŌŅ…Ķ√◊Óīů÷Ķ£ģ
‘Ő‚Ĺ‚őŲ£ļ£®1£©“Úő™x=3 Ī£¨y=4£Ľňý“‘a+3=4£¨Ķ√a=1
ĶĪ3£ľx°‹5 Ī£¨y=kx+7£®k£ľ0£©‘ŕ«Ýľš£®3£¨5]Ķ•ĶųĶ›ľű£¨ĶĪx=5 Ī£¨ymin=5k+7
“Úő™Ōķ ؾسŮx° £®3£¨5]ĪšĽĮ Ī£¨Ōķ ŘŃŅ◊ÓĶÕő™2∂÷£¨ňý“‘5k+7=2£¨Ķ√k=©Ā1
Ļ  £ģ
£ģ
£®2£©”…£®1£©÷™£¨ĶĪ1£ľx°‹3 Ī£¨
√Ņ»’Ōķ ŘņŻ»ů![]() =x3©Ā9x2+24x©Ā10£®1£ľx°‹3£©
=x3©Ā9x2+24x©Ā10£®1£ľx°‹3£©
f'£®x£©=3x2©Ā18x+24. ŃÓf'£®x£©=3x2©Ā18x+24£ĺ0£¨Ĺ‚Ķ√x£ĺ4ĽÚx£ľ2
ňý“‘f£®x£©‘ŕ[1£¨2]Ķ•ĶųĶ›‘Ų£¨‘ŕ[2£¨3]Ķ•ĶųĶ›ľű
ňý“‘ĶĪx=2£¨f£®x£©max=f£®2£©=10£¨
ĶĪ3£ľx°‹5 Ī£¨√Ņ»’Ōķ ŘņŻ»ůf£®x£©=£®©Āx+7£©£®x©Ā1£©=©Āx2+8x©Ā7=©Ā£®x©Ā4£©2+9
f£®x£©‘ŕx=4 Ī”–◊Óīů÷Ķ£¨«“f£®x£©max=f£®4£©=9£ľf£®2£©
◊Ř…Ō£¨Ōķ ؾسŮx=2ÕÚ‘™/∂÷ Ī£¨√Ņ»’Ōķ Řł√…Ő∆∑ňýĽŮņŻ»ů◊Óīů£ģ


 ŐžŐžŌÚ…Ō“ĽĪĺļ√ĺŪŌĶŃ–īūįł
ŐžŐžŌÚ…Ō“ĽĪĺļ√ĺŪŌĶŃ–īūįł –°—ß…ķ10∑÷÷””¶”√Ő‚ŌĶŃ–īūįł
–°—ß…ķ10∑÷÷””¶”√Ő‚ŌĶŃ–īūįł
| ńÍľ∂ | łŖ÷–Ņő≥Ő | ńÍľ∂ | ≥ű÷–Ņő≥Ő |
| łŖ“Ľ | łŖ“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű“Ľ | ≥ű“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ∂Ģ | łŖ∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű∂Ģ | ≥ű∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ»ż | łŖ»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű»ż | ≥ű»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° |
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™‘໿ņ‚◊∂![]() ÷–£¨
÷–£¨![]() ∑÷Īū «
∑÷Īū «![]() Ķń÷–Ķ„£¨
Ķń÷–Ķ„£¨![]() ∂ľ «’ż»żĹ«–ő£¨
∂ľ «’ż»żĹ«–ő£¨![]() .
.
£®1£©«ů÷§£ļ![]() ∆Ĺ√ś
∆Ĺ√ś![]() £Ľ
£Ľ
£®2£©«ů∂Ģ√śĹ«![]() Ķń∆Ĺ√śĹ«Ķń”ŗŌ“÷Ķ£Ľ
Ķń∆Ĺ√śĹ«Ķń”ŗŌ“÷Ķ£Ľ
£®3£©»ŰĶ„![]() ‘ŕ“ĽłŲĪŪ√śĽżő™
‘ŕ“ĽłŲĪŪ√śĽżő™![]() Ķń«Ú√ś…Ō£¨«ů
Ķń«Ú√ś…Ō£¨«ů![]() ĶńĪŖ≥§.
ĶńĪŖ≥§.
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™ļĮ ż![]() °£
°£
£®1£©ĶĪ![]() Ī£¨«ůļĮ ż
Ī£¨«ůļĮ ż![]() ‘ŕĶ„
‘ŕĶ„![]() ī¶Ķń«–ŌŖ∑Ĺ≥Ő£Ľ
ī¶Ķń«–ŌŖ∑Ĺ≥Ő£Ľ
£®2£©»ŰļĮ ż![]() £¨Ő÷¬ŘļĮ ż
£¨Ő÷¬ŘļĮ ż![]() ĶńĶ•Ķų–‘£Ľ
ĶńĶ•Ķų–‘£Ľ
£®3£©»Ű£®2£©÷–ļĮ ż![]() ”–ŃĹłŲľę÷ĶĶ„
”–ŃĹłŲľę÷ĶĶ„![]()
![]() £¨«“≤ĽĶ» Ĺ
£¨«“≤ĽĶ» Ĺ![]() ļ„≥…ŃĘ£¨«ů Ķ ż
ļ„≥…ŃĘ£¨«ů Ķ ż![]() Ķń»°÷Ķ∑∂őß.
Ķń»°÷Ķ∑∂őß.
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™Õ÷‘≤![]() Ķń◊ů°Ę”“ĹĻĶ„∑÷Īūő™
Ķń◊ů°Ę”“ĹĻĶ„∑÷Īūő™![]() £¨
£¨
÷ĪŌŖ![]() ”ŽÕ÷‘≤
”ŽÕ÷‘≤![]() Ķń“ĽłŲĹĽĶ„ő™
Ķń“ĽłŲĹĽĶ„ő™![]() £¨Ķ„
£¨Ķ„![]() «Õ÷‘≤
«Õ÷‘≤![]() …ŌĶń»ő“‚°™Ķ„£¨—”≥§
…ŌĶń»ő“‚°™Ķ„£¨—”≥§![]() ĹĽÕ÷‘≤
ĹĽÕ÷‘≤![]() ”ŕĶ„
”ŕĶ„![]() £¨Ń¨Ĺ”
£¨Ń¨Ĺ”![]() .
.
£®1£©«ůÕ÷‘≤![]() Ķń∑Ĺ≥Ő£Ľ
Ķń∑Ĺ≥Ő£Ľ
£®2£©«ů![]() Ķńńŕ«–‘≤Ķń◊Óīů÷‹≥§.
Ķńńŕ«–‘≤Ķń◊Óīů÷‹≥§.
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°ŅĽķī≤≥ßĹŮńÍńÍ≥ű”√98ÕÚ‘™ĻļĹÝ“ĽŐ® żŅōĽķī≤£¨≤ĘŃĘľīÕ∂»Ž…ķ≤ķ Ļ”√£¨ľ∆ĽģĶŕ“ĽńÍő¨–ř°ĘĪ£—Ý∑—”√12ÕÚ‘™£¨ī”Ķŕ∂ĢńÍŅ™ ľ£¨√ŅńÍňý–Ťő¨–ř°ĘĪ£—Ý∑—”√Ī»…Ō“ĽńÍ‘Ųľ”4ÕÚ‘™£¨ł√Ľķī≤ Ļ”√ļů£¨√ŅńÍĶń◊‹ ’»Žő™50ÕÚ‘™£¨…Ť Ļ”√xńÍļů żŅōĽķī≤Ķń”ĮņŻ∂Óő™yÕÚ‘™£ģ
(ĘŮ)–ī≥Ųy”Žx÷ģľšĶńļĮ żĻōŌĶ Ĺ£Ľ
(ĘÚ)ī”ĶŕľłńÍŅ™ ľ£¨ł√Ľķī≤Ņ™ ľ”ĮņŻ£®”ĮņŻ∂Óő™’ż÷Ķ£©£Ľ
(Ęů) Ļ”√»Űł…ńÍļů£¨∂‘Ľķī≤Ķńī¶ņŪ∑Ĺįł”–ŃĹ÷÷£ļ
(1)ĶĪńÍ∆Ĺĺý”ĮņŻ∂ÓīÔĶĹ◊Óīů÷Ķ Ī£¨“‘30ÕÚ‘™ľŘłŮī¶ņŪł√Ľķī≤£Ľ
(2)ĶĪ”ĮņŻ∂ÓīÔĶĹ◊Óīů÷Ķ Ī£¨“‘12ÕÚ‘™ľŘłŮī¶ņŪł√Ľķī≤£ģ
«Žń„—–ĺŅ“ĽŌ¬ńń÷÷∑Ĺįłī¶ņŪĹŌő™ļŌņŪ£Ņ«ŽňĶ√ųņŪ”…£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™ļĮ ż![]() £ģ
£ģ
£®1£©»Ű![]() £¨«ů«ķŌŖ
£¨«ů«ķŌŖ![]() ‘ŕĶ„
‘ŕĶ„![]() ī¶Ķń«–ŌŖ∑Ĺ≥Ő£Ľ
ī¶Ķń«–ŌŖ∑Ĺ≥Ő£Ľ
£®2£©»Ű![]() £¨«ů
£¨«ů![]() ‘ŕ«Ýľš
‘ŕ«Ýľš![]()
![]() …ŌĶń◊Ó–°÷Ķ£Ľ
…ŌĶń◊Ó–°÷Ķ£Ľ
£®3£©»ŰļĮ ż![]() ”–ŃĹłŲľę÷ĶĶ„
”–ŃĹłŲľę÷ĶĶ„![]() £¨«ů÷§£ļ
£¨«ů÷§£ļ![]() .
.
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
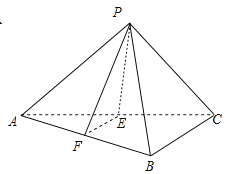
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨”–“ĽłŲ’ż»żņ‚◊∂ĶńŃ„ľĢ£¨P «≤ŗ√śACD…ŌĶń“ĽĶ„£ģ
ĻżĶ„P◊ų“ĽłŲ”Žņ‚ABīĻ÷ĪĶńĹō√ś£¨‘ű—ýĽ≠∑®£Ņ≤ĘňĶ√ųņŪ”…£ģ

≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ°įĹ°≤Ĺ◊Ŗ°Ī «“Ľ÷÷∑ĹĪ„∂Ý”÷”––ßĶń∂ÕŃ∂∑Ĺ Ĺ£¨ņÓņŌ ¶√ŅŐžľŠ≥÷°įĹ°≤Ĺ◊Ŗ°Ī£¨≤Ę”√ľ∆≤Ĺ∆ųĹÝ––Õ≥ľ∆£ģňŻ◊ÓĹŁ8Őž°įĹ°≤Ĺ◊Ŗ°Ī≤Ĺ żĶńŐű–őÕ≥ľ∆ÕľľįŌŗ”¶ĶńŌŻļńń‹ŃŅ żĺ›ĪŪ»ÁŌ¬£ļ


£®1£©«ůņÓņŌ ¶’‚8Őž°įĹ°≤Ĺ◊Ŗ°Ī≤Ĺ żĶń∆Ĺĺý ż£Ľ
£®2£©ī”≤Ĺ żő™16«ß≤Ĺ£¨17«ß≤Ĺ£¨18«ß≤ĹĶń6Őž÷–»ő—°2Őž£¨…ŤņÓņŌ ¶’‚2ŐžÕ®Ļż°įĹ°≤Ĺ◊Ŗ°ĪŌŻļńĶńń‹ŃŅļÕő™![]() £¨«ů
£¨«ů![]() Ķń∑÷≤ľŃ–ľį ż—ß∆ŕÕŻ£ģ
Ķń∑÷≤ľŃ–ľį ż—ß∆ŕÕŻ£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°ŅŌ¬Ń–ňĶ∑®’ż»∑Ķń «£® £©
A.‘≤◊∂ĶńĶ◊√ś «‘≤√ś£¨≤ŗ√ś ««ķ√ś
B.”√“Ľ’Ň…»–őĶń÷Ĺ∆¨Ņ…“‘ĺŪ≥…“ĽłŲ‘≤◊∂
C.“ĽłŲőÔŐŚ…Ō°ĘŌ¬ŃĹłŲ√ś «ŌŗĶ»Ķń‘≤√ś£¨ń«√īňŁ“Ľ∂® «“ĽłŲ‘≤÷ý
D.‘≤Ő®Ķń»ő“‚ŃĹŐűńłŌŖĶń—”≥§ŌŖŅ…ń‹ŌŗĹĽ“≤Ņ…ń‹≤ĽŌŗĹĽ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ļķľ —ß–£”Ň—° - Ń∑Ōį≤ŠŃ–ĪŪ - ‘Ő‚Ń–ĪŪ
ļĢĪĪ °Ľ•Ń™ÕÝő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®∆ĹŐ® | ÕÝ…Ō”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | ĶÁ–Ň’©∆≠ĺŔĪ®◊®«Ý | …śņķ ∑–ťőř÷ų“Ś”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | …ś∆ů«÷»®ĺŔĪ®◊®«Ý
ő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®ĶÁĽį£ļ027-86699610 ĺŔĪ®” Ōš£ļ58377363@163.com