
【题目】如图,有一个正三棱锥的零件,P是侧面ACD上的一点.
过点P作一个与棱AB垂直的截面,怎样画法?并说明理由.

【答案】详见解析.
【解析】试题分析:取![]() 中点
中点![]() ,可利用直线与平面垂直的判定定理,可证得
,可利用直线与平面垂直的判定定理,可证得![]() 平面
平面![]() ,过点
,过点![]() 与
与![]() 平行的直线与平面
平行的直线与平面![]() ,进而与
,进而与![]() 垂直。
垂直。
(方法一)
画法:过点P在面ACD内作EF//CD,交AC于E点,交AD于F点.
过E作EG⊥AB,连接FG,平面EFG为所求.
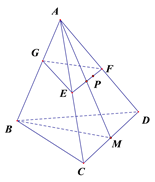 理由:取CD中点M,连接AM,BM.
理由:取CD中点M,连接AM,BM.
∵A-BCD为正三棱锥,
∴AC=AD,BC=BD,
∴BM⊥CD,AM⊥CD ,
AM∩BM=M,
AM![]() 平面ABM ,BM
平面ABM ,BM![]() 平面ABM,
平面ABM,
∴CD⊥平面ABM .
∵AB![]() 平面ABM,
平面ABM,
∴CD⊥AB.
∵EF∥CD,
∴EF⊥AB .
过E作EG⊥AB,连接FG,
∵EF∩EG=E .
EF![]() 面EFG,EG
面EFG,EG![]() 面EFG,
面EFG,
![]() AB⊥面EFG .
AB⊥面EFG .
(方法二)
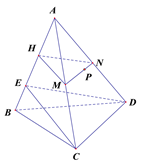
画法:过C在平面ABC内M作CE⊥AB,垂足为E.连接DE.
过点P作MN // CD,交AC于M,AD于N.
过M作MH//CE,交AE于H,连接HN,平面HMN为所求.
理由:![]() ,
,
![]() .
.
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
由画法知, AB⊥HM,
∵HM∩HN=H,
HM![]() 面MNH,HN
面MNH,HN![]() 面MNH,
面MNH,
![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最小值和最大值;
上的最小值和最大值;
(2)当![]() 时,讨论函数
时,讨论函数![]() 的单调性;
的单调性;
(3)是否存在实数![]() ,对任意的
,对任意的![]() ,且
,且![]() ,都有
,都有![]() 恒成立,若存在,求出
恒成立,若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某种商品每日的销售量y(单位:吨)与销售价格x(单位:万元/吨,1<x≤5)满足:当1<x≤3时,y=a(x﹣4)2 +![]() (a为常数);当3<x≤5时,y=kx+7(k<0),已知当销售价格为3万元/吨时,每日可售出该商品4吨,且销售价格x∈(3,5]变化时,销售量最低为2吨.
(a为常数);当3<x≤5时,y=kx+7(k<0),已知当销售价格为3万元/吨时,每日可售出该商品4吨,且销售价格x∈(3,5]变化时,销售量最低为2吨.
(1)求a,k的值,并确定y关于x的函数解析式;
(2)若该商品的销售成本为1万元/吨,试确定销售价格x的值,使得每日销售该商品所获利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在原点,焦点在x轴上,离心率等于![]() ,它的一个顶点恰好是抛物线
,它的一个顶点恰好是抛物线![]() 的焦点,
的焦点,
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)过椭圆C的右焦点![]() 作直线l交椭圆C于A、B两点,交y轴于M点,若
作直线l交椭圆C于A、B两点,交y轴于M点,若![]()
![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列事件中,是必然事件的是( )
A.任意买一张电影票,座位号是2的倍数B.13个人中至少有两个人生肖相同
C.车辆随机到达一个路口,遇到红灯D.明天一定会下雨
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校举办运动会时,高一(1)班有28名同学参加比赛,有15人参加游泳比赛,有8人参加田径比赛,有14人参加球类比赛,同时参加游泳和田径比赛的有3人,同时参加游泳和球类比赛的有3人,没有人同时参加三项比赛.则同时参加田径和球类比赛的人数是( ).
A.3B.4C.5D.6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com