Question

10．已知D、E、F分别为△ABC的边BC、CA、AB的中点，且$\overrightarrow{BC}$=$\overrightarrow a$、$\overrightarrow{CA}$=$\overrightarrow b$、$\overrightarrow{AB}$=$\overrightarrow c$、则
①$\overrightarrow{EF}=\frac{1}{2}\overrightarrow c-\frac{1}{2}$$\overrightarrow b$；
②$\overrightarrow{BE}=\overrightarrow a+\frac{1}{2}$$\overrightarrow b$；
③$\overrightarrow{CF}=-\frac{1}{2}\overrightarrow a+\frac{1}{2}$$\overrightarrow b$；
④$\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF}$=$\overrightarrow 0$
其中正确的等式个数为（　　）

• A． 1
• B． 2
• C． 3
• D． 4

Answer 1

分析 根据向量加法和减法的运算法则进行化简即可．

解答 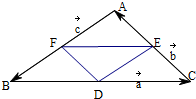解：①∵E、F分别为△ABC的边CA、AB的中点，
∴$\overrightarrow{EF}$=$\frac{1}{2}$$\overrightarrow{CB}$=$\frac{1}{2}$（$\overrightarrow{c}$-$\overrightarrow{b}$）=$\frac{1}{2}$$\overrightarrow{c}$-$\frac{1}{2}$$\overrightarrow{b}$，故①正确，
②$\overrightarrow{BE}$=$\overrightarrow{BC}+\overrightarrow{CE}$=$\overrightarrow{a}$+$\frac{1}{2}\overrightarrow{b}$，故②正确，
③$\overrightarrow{CF}$=$\overrightarrow{CA}+\overrightarrow{AF}$=$\overrightarrow{b}$+$\frac{1}{2}\overrightarrow{c}$，故③错误，
④$\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF}$=$\frac{1}{2}$（$\overrightarrow{c}$-$\overrightarrow{b}$）+$\frac{1}{2}$（$\overrightarrow{a}$-$\overrightarrow{c}$）+$\frac{1}{2}$（$\overrightarrow{b}$-$\overrightarrow{a}$）=$\overrightarrow 0$，故④正确，
故正确是①②④，共有3个，
故选：C

点评 本题主要考查向量的加法和加法的运算，根据三角形法则是解决本题的关键．