已知定义域为[0,1]的函数f(x)同时满足以下三个条件:
(1)对任意的x∈[0,1],总有f(x)>0;
(2)f(1)=1;
(3)若x1≥0,x2≥0,x1+x2≤1,则有f(x1+x2)≥f(x1)+f(x2)成立,则称f(x)为“友谊函数”,请解答下列各题:
①若已知f(x)为“友谊函数”,求f(0)的值并判断函数的单调性;
②函数g(x)=2x-1在区间[0,1]上是否为“友谊函数”?并给出理由.
【答案】
分析:①赋值可考虑取x
1=x
2=0,代入f(x
1+x
2)≥f(x
1)+f(x
2),可得f(0)≥f(0)+f(0),由已知f(0)≥0,可得f(0)=0,由0≤x
1<x
2≤1,则0<x
2-x
1<1,故有f(x
2)=f(x
2-x
1+x
1)≥f(x
2-x
1)+f(x
1)≥f(x
1),即得结论成立;
②要判断函数g(x)=2
x-1在区间[0,1]上是否为“友谊函数,只要检验函数g(x)=2
x-1在[0,1]上是否满足(1)g(x)>0;(2)g(1)=1;(3)x
1≥0,x
2≥0,且x
1+x
2≤1,有g(x
1+x
2)≥g(x
1)+g(x
2)即可.
解答:解:①取x
1=x
2=0,代入f(x
1+x
2)≥f(x
1)+f(x
2),
得f(0)≥f(0)+f(0),化简可得f(0)≤0
又由f(0)≥0,得f(0)=0
设0≤x
1<x
2≤1,则0<x
2-x
1<1,
所以f(x
2)=f(x
2-x
1+x
1)≥f(x
2-x
1)+f(x
1)≥f(x
1)
故有f(x
1)≤f(x
2),故函数f(x)为定义在[0,1]上的增函数;
②显然g(x)=2
x-1在[0,1]上满足(1)g(x)>0;(2)g(1)=1;(3)若x
1≥0,x
2≥0,且x
1+x
2≤1,则有
g(x
1+x
2)-[g(x
1)+g(x
2)]=

-1-[(
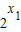
-1)+(
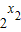
-1)]=(
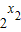
-1)(
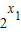
-1)≥0
故g(x)=2
x-1满足条件(1)、(2)、(3),
所以g(x)=2
x-1为友谊函数.
点评:采用赋值法是解决抽象函数的性质应用的常用方法,而函数的新定义往往转化为一般函数性质的研究,本题结合指数函数的性质研究函数的函数的函数值域的应用,指数函数的单调性的应用.

 -1-[(
-1-[(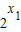 -1)+(
-1)+(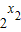 -1)]=(
-1)]=(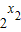 -1)(
-1)(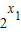 -1)≥0
-1)≥0

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案