练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在平面四边形ABCD中，∠A=∠B=∠C=75°，BC=2，则AB的取值范围是                    



    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    将一个四棱锥的每个顶点染上一种颜色，并使同一条棱上的两个端点异色，若只有4种颜色可供使用，则不同的染色方法总数有

        A．48种             B．72种             C．96种             D．108种

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若函数f（x）=是奇函数，则使f（x）>3成立的x的取值范围为

    （A）( )   (B)()  （C）（0,1） （D）（1，+）

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    投篮测试中，每人投3次，至少投中2次才能通过测试。已知某同学每次投篮投中的概率为0.6，且各次投篮是否投中相互独立，则该同学通过测试的概率为

           （A）0.648   （B）0.432           （C）0.36            （D）0.312

    查看答案和解析>>

    科目：高中数学 来源： 题型：


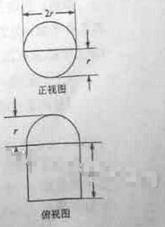
    圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体，该几何体三视图中的正视图和俯视图如图所示。若该几何体的表面积为16 + 20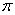，则r=

    （A）1（B）2（C）4（D）8

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f（x）=

    (Ⅰ)当a为何值时，x轴为曲线 的切线；

    （Ⅱ）用  表示m,n中的最小值，设函数 ，讨论h（x）零点的个数

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    等比数列｛an｝满足a1=3，a1+ a3+ a5=21，则a3+ a5+ a7 =

    （A）21      （B）42       （C）63     （D）84

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设函数f(x)=emx+x2-mx.

    (Ⅰ)证明：f(x)在（-∞，0）单调递减，在（0，+∞）单调递增；

    （Ⅱ）若对于任意x 1, x2∈[-1,1],都有｜f(x1)- f(x2)｜≤e-1,求m的取值范围

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图四边形ABCD为菱形，G为AC与BD交点，，

    （I）证明：平面平面；

    （II）若， 三棱锥的体积为，求该三棱锥的侧面积.

    查看答案和解析>>

    同步练习册答案