
分析 (1)由f(x)+1=-x2+(a-1)x+a=0,解得x=-1或x=a.即可判断出结论.
(2)f(x)=-x2+(a-1)x+a-1=0有2相异解实根时,△>0,解得a范围.g(x)=x(x-a)2-1=0,g′(x)=(x-a)(3x-a),对a分类讨论,利用导数研究其单调性即可得出.
解答 解:(1)由f(x)+1=-x2+(a-1)x+a=0,
解得x=-1或x=a.
当a∈(0,1)时,存在x0∈(0,1),使得f(x0)+1=0.
(2)f(x)=-x2+(a-1)x+a-1=0有2相异解实根时,
△=(a-1)2+4(a-1)>0,∴a<-3,或a>1.
g(x)=x(x-a)2-1=0,g′(x)=(x-a)(3x-a),
当a=0时,g′(x)≥0,g(x)=0有1解;
当a<0时,$a<\frac{a}{3}$,$g(x)在({-∞,a})上增,({a,\frac{a}{3}})上减,({\frac{a}{3},+∞})上增$,
极大值g(a)=-1<0,g(x)=0有1解;
当a>0时,$a>\frac{a}{3}$,$g(x)在({-∞,\frac{a}{3}})上增,({\frac{a}{3},a})上减,({a,+∞})上增$,
极小值g(a)=-1<0,
要使g(x)=0有3解,只须$g({\frac{a}{3}})>0$,∴$a>\frac{{3\root{3}{2}}}{2}$.
下面用反证法证明$a>\frac{{3\root{3}{2}}}{2}$时,5个根相异.
假设?x0∈R,f(x0)=g(x0)=0,
即$\left\{\begin{array}{l}-{x_0}^2+({a-1}){x_0}+a-1=0\\{x_0}{({{x_0}-a})^2}-1=0\end{array}\right.$两式相减得:$({{x_0}-a})({{x_0}^2-a{x_0}+{x_0}+1})=0$,
若x0=a代入②得0-1=0矛盾;
若${x_0}^2-a{x_0}+{x_0}+1=0$代入①得a=0,这与$a>\frac{{3\root{3}{2}}}{2}$矛盾.
∴假设不成立,即5个根相异.
综上,$a>\frac{{3\root{3}{2}}}{2}$.
点评 本题考查了利用导数研究函数单调性极值与最值、函数的零点、反证法、二次函数与判别式的关系,考查了分类讨论思想方法、推理能力与计算能力,属于难题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
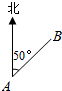 某人沿一条折线段组成的小路前进,从A到B,方位角(从正北方向顺时针转到AB方向所成的角)是50°,距离是3km;从B到C,方位角是110°,距离是3km;从C到D,方位角是140°,距离是($9+3\sqrt{3}$)km.
某人沿一条折线段组成的小路前进,从A到B,方位角(从正北方向顺时针转到AB方向所成的角)是50°,距离是3km;从B到C,方位角是110°,距离是3km;从C到D,方位角是140°,距离是($9+3\sqrt{3}$)km.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 方程x2+bx+a=0至多一个实根 | B. | 方程x2+bx+a=0有实根 | ||
| C. | 方程x2+bx+a=0至多有两个实根 | D. | 方程x2+bx+a=0恰好有两个实根 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com