
 某人沿一条折线段组成的小路前进,从A到B,方位角(从正北方向顺时针转到AB方向所成的角)是50°,距离是3km;从B到C,方位角是110°,距离是3km;从C到D,方位角是140°,距离是($9+3\sqrt{3}$)km.
某人沿一条折线段组成的小路前进,从A到B,方位角(从正北方向顺时针转到AB方向所成的角)是50°,距离是3km;从B到C,方位角是110°,距离是3km;从C到D,方位角是140°,距离是($9+3\sqrt{3}$)km.分析 (Ⅰ)连接AC通过余弦定理求得AC.
(Ⅱ)利用余弦定理求得AD,进而利用正弦定理求得sin∠CAD,求得∠CAD,则AD的方位角可得.
解答 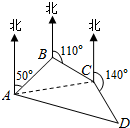 解:(Ⅰ)示意图,如图所示,
解:(Ⅰ)示意图,如图所示,
连接AC,在△ABC中,∠ABC=50°+(180°-110°)=120°,
又AB=BC=3,∴∠BAC=∠BCA=30°
由余弦定理可得
AC=$\sqrt{A{B}^{2}+B{C}^{2}-2AB•BC•cos120°}$=3$\sqrt{3}$
(Ⅱ)在△ACD中,∠ACD=360°-140°-(70°+30°)=120°,CD=3$\sqrt{3}$+9.
由余弦定理得AD=$\sqrt{A{C}^{2}+C{D}^{2}-2AC•CD•cos120°}$=$\sqrt{27+(3\sqrt{3}+9)^{2}-2×3\sqrt{3}×(3\sqrt{3}+9)×(-\frac{1}{2})}$
=9$\sqrt{2+\sqrt{3}}$=$\frac{9(\sqrt{2}+\sqrt{6}}{2}$(km).
由正弦定理得sin∠CAD=$\frac{CD•sin∠ACD}{AD}$=$\frac{\sqrt{2}}{2}$
∴∠CAD=45°,于是AD的方位角为50°+30°+45°=125°,
所以,从A到D的距离为$\frac{9(\sqrt{2}+\sqrt{6})}{2}$km,方位角是125°.
点评 本题主要考查了解三角形的知识,方位角的概念和余弦定理的应用.要求学生对实际问题能准确建模.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 45 | B. | $\frac{π}{2}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
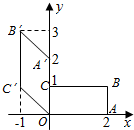 如图,矩形OABC在变换T的作用下变成了平行四边形OA′B′C′,变换T所对应的矩阵为M,矩阵N是把坐标平面上的点的横坐标伸长到原来的2倍,纵坐标伸长到原来的3倍的变换所对应的矩阵.
如图,矩形OABC在变换T的作用下变成了平行四边形OA′B′C′,变换T所对应的矩阵为M,矩阵N是把坐标平面上的点的横坐标伸长到原来的2倍,纵坐标伸长到原来的3倍的变换所对应的矩阵.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com