
分析 (1)求得a=1的函数的解析式,讨论x的范围,去绝对值,由对称轴和区间的关系,可得f(x)的单调增区间;
(2)对a讨论,当$\frac{3}{2}$<a≤2时,当1<a≤$\frac{3}{2}$时,当$\frac{1}{2}≤a≤1$时,化简函数f(x),求得对称轴和最大值,运用参数分离和二次函数的最值求法,即可得到b的范围.
解答 解:(1)由a=1,可得f(x)=-x2+2x+2|x-1|+b,
当x≥1时,f(x)=-x2-2+4x+b=-(x-2)2+b+2,
当x<1时,f(x)=-x2+2+b,
得单调递增区间为(-∞,0),(1,2);
(2)(i)当$\frac{3}{2}$<a≤2时,f(x)=-x2+2(1-a)x+2a2+b,
因为对称轴$x=1-a<-\frac{1}{2}$,$f{(x)_{max}}=f(-\frac{1}{2})<0$恒成立,
得$b<-2{a^2}-a+\frac{5}{4}$在$a∈(\frac{3}{2},2]$上恒成立,又${(-2{a^2}-a+\frac{5}{4})_{min}}=-\frac{35}{4}$,
∴b<-$\frac{35}{4}$;
(ii)当1<a≤$\frac{3}{2}$时,f(x)=-x2+2(1-a)x+2a2+b,
因为对称轴x=1-a∈[-$\frac{1}{2}$,0],f(x)max=f(1-a)<0恒成立,
得b<-3a2+2a-1在$a∈(1,\frac{3}{2}]$上恒成立,
又${(-3{a^2}+2a-1)_{min}}=-\frac{19}{4}$,
∴$b<-\frac{19}{4}$;
(iii)当$\frac{1}{2}≤a≤1$时,x<a时,对称轴x=1-a∈[0,$\frac{1}{2}$],f(x)max=f(1-a)
x≥a时,对称轴x=1+a∈[$\frac{3}{2}$,2],f(x)max=f(1),
所以,$\left\{\begin{array}{l}{f(1-a)<0}\\{f(1)<0}\end{array}\right.$即有$\left\{\begin{array}{l}{b<-3{a}^{2}+2a-1}\\{b<2{a}^{2}-2a-1}\end{array}\right.$,
在$\frac{1}{2}$≤a≤1上恒成立,可得$\left\{\begin{array}{l}{(-3{a}^{2}+2a-1)_{min}=-2}\\{(2{a}^{2}-2a-1)_{min}=-\frac{3}{2}}\end{array}\right.$可得b<-2,
综上可得,实数b的取值范围是b<-$\frac{35}{4}$.
点评 本题考查绝对值函数的性质和运用,主要考查单调区间的求法和二次函数的最值问题,注意讨论对称轴和区间的关系,属于中档题.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:解答题
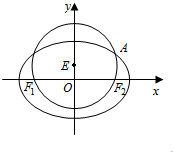 已知圆E:x2+(y-$\frac{1}{2}$)2=$\frac{9}{4}$经过椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点F1,F2,且与椭圆C在第一象限的交点为A,且F1,E,A三点共线,直线l交椭圆C于M,N两点,且$\overrightarrow{MN}$=λ$\overrightarrow{OA}$(λ≠0)
已知圆E:x2+(y-$\frac{1}{2}$)2=$\frac{9}{4}$经过椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点F1,F2,且与椭圆C在第一象限的交点为A,且F1,E,A三点共线,直线l交椭圆C于M,N两点,且$\overrightarrow{MN}$=λ$\overrightarrow{OA}$(λ≠0)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈(-∞,0),x2-ax+4>0 | B. | ?x∈(-∞,0),x2-ax+4>0 | ||
| C. | ?x∈(0,+∞),x2-ax+4≤0 | D. | ?x∈(0,+∞),x2-ax+4≤0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
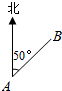 某人沿一条折线段组成的小路前进,从A到B,方位角(从正北方向顺时针转到AB方向所成的角)是50°,距离是3km;从B到C,方位角是110°,距离是3km;从C到D,方位角是140°,距离是($9+3\sqrt{3}$)km.
某人沿一条折线段组成的小路前进,从A到B,方位角(从正北方向顺时针转到AB方向所成的角)是50°,距离是3km;从B到C,方位角是110°,距离是3km;从C到D,方位角是140°,距离是($9+3\sqrt{3}$)km.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com