
分析 由和差角的公式变形已知式子可得tanx=$\frac{sin40°}{cos40°+2sin10°}$,再由和差角的公式化简即可.
解答 解:∵sin(x-40°)=cos(x+10°)-cos(x-10°),
∴sinxcos40°-cosxsin40°=cosxcos10°-sinxsin10°-cosxcos10°-sinxsin10°,
∴sinxcos40°-cosxsin40°=-2sinxsin10°,
∴(cos40°+2sin10°)sinx=cosxsin40°,
∴tanx=$\frac{sinx}{cosx}$=$\frac{sin40°}{cos40°+2sin10°}$=$\frac{sin40°}{cos(30°+10°)+2sin10°}$
=$\frac{sin40°}{\frac{\sqrt{3}}{2}cos10°-\frac{1}{2}sin10°+2sin10°}$=$\frac{sin40°}{\frac{\sqrt{3}}{2}cos10°+\frac{3}{2}sin10°}$
=$\frac{sin40°}{\sqrt{3}(\frac{1}{2}cos10°+\frac{\sqrt{3}}{2}sin10°)}$=$\frac{sin40°}{\sqrt{3}sin(30°+10°)}$=$\frac{\sqrt{3}}{3}$
故答案为:$\frac{{\sqrt{3}}}{3}$
点评 本题考查和差角的三角函数公式,熟练应用公式是解决问题的关键,属中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
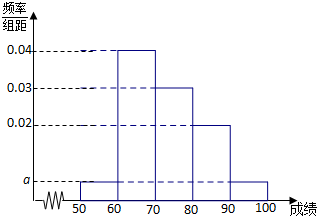 某校1000名学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
某校1000名学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].| 分数段 | [50,60) | [60,70) | [70,80) | [80,90) |
| x:y | 1:1 | 4:5 | 3:2 | 2:1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com