
分析 由奇函数f(x)与g(x)偶函数的定义域都为(-∞,+∞),且满足f(x)+g(x)=2x,可得2-x=f(-x)+g(-x)=-f(x)+g(x),解得f(x)=$\frac{{2}^{x}-{2}^{-x}}{2}$,g(x)=$\frac{{2}^{x}+{2}^{-x}}{2}$.
①利用基本不等式的性质即可判断出正误;
②把f(x)=$\frac{{2}^{x}-{2}^{-x}}{2}$,g(x)=$\frac{{2}^{x}+{2}^{-x}}{2}$代入f(x)2-g(x)2化简整理即可判断出正误;
③f(x)=$\frac{{2}^{x}-{2}^{-x}}{2}$≤$\frac{{2}^{x}+{2}^{-x}}{2}$=g(x),即可判断出正误;
④分别计算g(2x)=$\frac{{4}^{x}+{4}^{-x}}{2}$,2f(x)g(x)=$\frac{{4}^{x}-{4}^{-x}}{2}$.即可判断出正误.
解答 解:∵奇函数f(x)与g(x)偶函数的定义域都为(-∞,+∞),且满足f(x)+g(x)=2x,
∴2-x=f(-x)+g(-x)=-f(x)+g(x),解得f(x)=$\frac{{2}^{x}-{2}^{-x}}{2}$,g(x)=$\frac{{2}^{x}+{2}^{-x}}{2}$.
①∵g(x)=$\frac{{2}^{x}+{2}^{-x}}{2}$$≥\sqrt{{2}^{x}•{2}^{-x}}$=1,当且仅当x=0时取等号,因此g(x)≥1在(-∞,+∞)恒成立,①正确;
②f(x)2-g(x)2=$(\frac{{2}^{x}-{2}^{-x}}{2})^{2}$-$(\frac{{2}^{x}+{2}^{-x}}{2})^{2}$=-1在(-∞,+∞)恒成立,②正确;
③f(x)=$\frac{{2}^{x}-{2}^{-x}}{2}$≤$\frac{{2}^{x}+{2}^{-x}}{2}$=g(x),因此f(x)≤g(x)在(-∞,+∞)恒成立,③正确;
④g(2x)=$\frac{{4}^{x}+{4}^{-x}}{2}$,2f(x)g(x)=2×$\frac{{2}^{x}-{2}^{-x}}{2}$×$\frac{{2}^{x}+{2}^{-x}}{2}$=$\frac{{4}^{x}-{4}^{-x}}{2}$.∴g(2x)≠2f(x)g(x),④不正确.
故答案为:①②③.
点评 本题考查了函数的奇偶性、单调性、基本不等式的性质、简易逻辑的判定,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
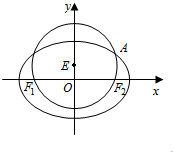 已知圆E:x2+(y-$\frac{1}{2}$)2=$\frac{9}{4}$经过椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点F1,F2,且与椭圆C在第一象限的交点为A,且F1,E,A三点共线,直线l交椭圆C于M,N两点,且$\overrightarrow{MN}$=λ$\overrightarrow{OA}$(λ≠0)
已知圆E:x2+(y-$\frac{1}{2}$)2=$\frac{9}{4}$经过椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点F1,F2,且与椭圆C在第一象限的交点为A,且F1,E,A三点共线,直线l交椭圆C于M,N两点,且$\overrightarrow{MN}$=λ$\overrightarrow{OA}$(λ≠0)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com