
分析 先分别求得p为真命题,q为真命题时,a的范围,再根据命题p或q为真命题,p且q为假命题,可得p和q有且只有一个是真命题,从而分p真q假,p假 q真,分别求得a的范围,最后求出它们的并集即可.
解答 解:对任意实数x都有x2+ax+a>0恒成立?△<0?0<a<4
命题p:?0<a<4…(2分)
关于x的方程x2-x+a=0有实数根?△≥0?1-4a≥0?a≤$\frac{1}{4}$;
命题q:$?a≤\frac{1}{4}$…(4分)
∵“p或q”为真命题,“p且q”为假命题,
∴p与q一真一假.…(6分)
如果p真,q假$?\left\{\begin{array}{l}0<a<4\\ a>\frac{1}{4}\end{array}\right.?\frac{1}{4}<a<4$;…(8分)
如果p假q真$?\left\{\begin{array}{l}a≤0或a≥4\\ a≤\frac{1}{4}\end{array}\right.?a≤0$…(10分)
所以实数a的取值范围为$({-∞,0}]∪({\frac{1}{4},4})$…(12分)
点评 本题以命题为载体,考查复合命题的真假运用,解题的关键是根据命题p或q为真命题,p且q为假命题,可得p和q有且只有一个是真命题,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈(-∞,0),x2-ax+4>0 | B. | ?x∈(-∞,0),x2-ax+4>0 | ||
| C. | ?x∈(0,+∞),x2-ax+4≤0 | D. | ?x∈(0,+∞),x2-ax+4≤0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{200}{3}$m | B. | $\frac{200\sqrt{3}}{3}$m | C. | $\frac{400}{3}$m | D. | $\frac{400\sqrt{3}}{3}$m |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
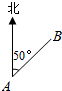 某人沿一条折线段组成的小路前进,从A到B,方位角(从正北方向顺时针转到AB方向所成的角)是50°,距离是3km;从B到C,方位角是110°,距离是3km;从C到D,方位角是140°,距离是($9+3\sqrt{3}$)km.
某人沿一条折线段组成的小路前进,从A到B,方位角(从正北方向顺时针转到AB方向所成的角)是50°,距离是3km;从B到C,方位角是110°,距离是3km;从C到D,方位角是140°,距离是($9+3\sqrt{3}$)km.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com